Приклад.

Тема 13. Визначений інтеграл.

Якщо при будь-якому розбитті відрізка [ а,b ] такому, що maxDx_i® 0 і довільному виборі точок e_i інтегральна сума прагне до границі S, яка називається визначеним інтегралом від f(x) на відрізку [ а, b ].

Позначення:

Властивості визначеного інтеграла.

1)

2)

3)

4) Якщо f(x) £ j(x) на відрізку [а, b] а < b, то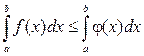

5) Якщо m і M – відповідно найменше і найбільше значення функції f(x) на відрізку [а, b], то:

6) Теорема про середнє. Якщо функція f(x) безперервна на відрізку [ а,b ], то на цьому відрізку існує точка e така, що

7) Для довільних чисел а, b, с справедлива рівність:

Зрозуміло, ця рівність виконується, якщо існує кожний з інтегралів, що входять до неї.

8)

Теорема: (Теорема Ньютона – Лейбніца)

Якщо функція F(x) – будь-яка первісна від безперервної функції f(x), то

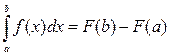
Цей вираз відомий під назвою формули Ньютона – Лейбніца.

Формула Ньютона – Лейбніца є загальним підходом до знаходження визначених інтегралів.

Що стосується прийомів обчислення визначених інтегралів, то вони практично нічим не відрізняються від всіх тих прийомів і методів, які були розглянуті вище при знаходженні невизначених інтегралів.

Так само застосовуються методи підстановки (заміни змінної), метод інтегрування по частинах, ті ж прийоми знаходження первісних для тригонометричних, ірраціональних і трансцендентних функцій. Особливістю є тільки те, що при застосуванні цих прийомів треба поширювати перетворення не тільки на підінтегральну функцію, але і на границі інтегрування. Замінюючи змінну інтегрування, не треба забувати змінити відповідно границі інтегрування.

Приклади. Знайти визначені інтеграли

1. ;

2. ;

3. ;

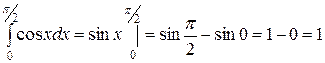4. .

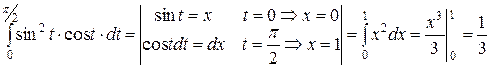Якщо функції u=j(x) і v=y(x) безперервні на відрізку [а, b], а також безперервні на цьому відрізку їх похідні, то справедлива формула інтегрування частинами:

Приклад Обчислимо інтеграл

Вигідно узяти і , так що одержимо:

При цьому виниклий позаінтегральний член ми обчислили так:

.

Особливо ясно виявляється вказана в зауваженні перевага в тому випадку, якщо формулу інтегрування частинами доводиться застосовувати кілька разів підряд.

Дата добавления: 2015-07-12