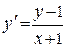
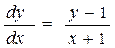
Приклад. Заміняємо на : , змінні

Заміняємо на : , змінні

розділилися. Інтегруємо: ;

,

- загальне рішення.

Диференціальне рівняння

(14.3)

називається лінійним диференціальним рівнянням першого порядку (у й у' входять у перших ступенях, не перемножуючись між собою). Якщо q(x)≡0, той рівняння називається лінійним однорідним, якщо q(x)≠0, то рівняння називається неоднорідним.

Загальне рішення лінійного однорідного рівняння легко виходить поділом змінних:

,

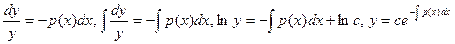де С – довільна постійна.

Загальне рішення лінійного неоднорідного рівняння можна знайти виходячи із загального рішення відповідного однорідного рівняння методом Лагранжа, варіюючи довільну постійну, тобто починаючи , де С(х) – деяка диференцируєма функція від х, що підлягає визначенню.

Для знаходження С(х) потрібно підставити в у вихідне рівняння:

, де С – довільна постійна. Тоді рішення неоднорідного рівняння, яке шукається, має вигляд:

.

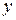Лінійні диференціальні рівняння першого порядку можна інтегрувати також методом Бернуллі, який полягає в наступному. Робимо заміну , де – функції від x. Тому що , те після підстановки й у рівняння (14.3), одержуємо або, групуючи члени,

Функцію виберемо так, щоб виконувалася рівність , або . Нехай рішенням цього диференціального рівняння з розділеними змінними 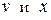є функція 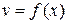, тоді при такому виборі функції v одержуємо диференціальне рівняння з змінними, що розділяються 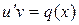або , 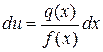. Нехай загальним рішенням цього рівняння є функція , тоді функція - загальне рішення рівняння (14.3).

Отже згідно з методом Бернуллі, рішення лінійного диференціального рівняння першого порядку зводиться до послідовного рішення двох рівнянь із змінними, що розділяються:

y=uv

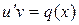і - функція, яка шукалася.

Приклад.

Переконаємося, що рівняння лінійне першого порядку щодо шуканої функції , причому Робимо заміну тоді . Підставляємо y і в останнє рівняння: Групуємо Функцію v знаходимо з умови . Розділяємо змінні v і x:

або , .

Інтегруючи останнє рівняння, знаходимо ,

. одержуємо зі згрупованого рівняння, що або

Скорочуємо на : , . Таким чином, загальним рішенням заданого рівняння є функція .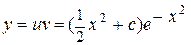

Приклад.

Спочатку представимо рівняння в стандартному виді:

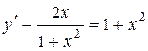
Переконаємося, що воно лінійне першого порядку щодо шуканої функції у(x) . Далі надходимо по шаблонові. Робимо заміну . В останнє рівняння підставляємо нові значення 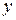і й групуємо члени:

, далі, вирішуємо диференціальне рівняння

, , тому що , то одержуємо, що , , . Вирішуючи диференціальне рівняння , знаходимо u: 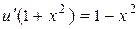, , , де c – постійна інтегрування. Таким чином, - загальне рішення.

ЗАВДАННЯ ДО САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ

Дата добавления: 2015-07-12