Эксперементальное определение структуры кристаллов.

Атомное строение кристалла определяется по дифракции рассеянию рентгеновских лу-чей, ē, нейтронов. Развитие структурного анализа началось с опыта М. Мауре (1912г.), которая показала, что пучок рентгеновских лучей, проходя через кристалл, испытывает дифракцию. Симметрия распределения дифракционных максимумов (пятен на фотоплас-тинки) будет соответствовать симметрии кристалла. Кристаллы с их трехмерными пери-одическими структурами являются естественными дифракционными решетками для рентгеновских лучей, так как длины волн с межатомными расстояниями кристалла. Диф-ракционные максимумы возникают во всех направлениях, для которых справедливо уравнение Вульфа - Брегга.

2dsinά=nλ, n=1,2,3...

Согласно условию В-Брегга дифракционный максимум получается только для опреде-ленных напряжений и межплокостных расстояний.

d-межплоскостное расстояние

Методы рентгеноструктурного анализа делят на 2 в зависимости от условий съем-ки:1) когда угол падения - постоянен, меняют длину волны; 2) длина волны - постоянна, меняют угол падения. Отраженный от кристалла пучок регистрируется на фотоприем-нике специальным счетчиком.

Первый метод: метод Лауре

На кристалл, ориентированный под определенным углом к пучку, падает пучок немоно-хроматического излучения, причем каждая длина волны должна удовлетворять условию В-Брегга. Такой метод применяют для ориентировки кристалла и его симметрии.

Второй метод осуществляется двумя способами:

- метод вращения - заключается в том, что кристалл вращают вокруг оси перпен-дикулярно монохроматическому пучку. Т.О. различные плоскости кристалла ставятся последовательно в положение, соответствующее условию дифракции.

- метод Дебая - Шеррера - поликристалл или мелкий порошок из монокристаллических зерен осветвляется монохроматическим излучением. Во множестве произвольнл ориен-тированных монокристаллов, всегда найдутся такие, ориентировка которых удовлетво-ряет условию В-Брегга.

Рентгеновское излучение получается путем бомбардировки медной пластины быстрыми электронами

для меди λ=1,541Å

для молибдена λ=0,709Å

1Å=

Для мсследования кристалла требуется рентгеновское излучение с энергией кванта .

Сложные структуры порядка 10000 отражений, и в ходе такого анализа определить координату от 500 до 5000 атомов.

По дифракционной координате можно судить о геометрии решетки. По интенсив-ности можно судить о распределении атомов.

Рентгеноструктурный анализ распадается на два этапа:

1 - определение геометрии структуры

2 - выдевание этой пространственной группы конкретным набором различных атомов.

Интенсивность рассеяния атомов зависит от типа атома и его положения в ячейки. Интенсивность дифракционных максимумов измеряется по степени почернения фото-пластинки или точными автоматическими методами. Определяя интенсивность диф-ракционных максимумов, по ним определяем распределение электронной плотности, то есть максимальную вероятность нахождения электрона в той или иной точке крис-талла. Распределение электронной плотности устанавливают методами гармоническо-го анализа. По интенсивности рассеяния рентгеновских лучей в кристалле измеряют υ распределения упругих волн, анизотропию кристалла. Кроме того - наблюдения дефектов структуры кристаллов.

Схема для определения структуры кристалла

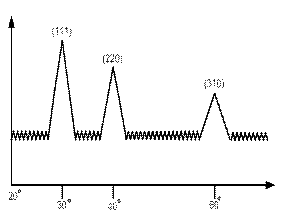
Схема камеры, использующаася Порошковая нейтронограмма алмаза

для рентгеновской дифракции.

- пленка

Межплоскостное расстояние определяется для отдельных плоскостей hkl:

(параметрической ячейки)

Параметры обратной решетки а,b,с,

Каждый узел прямой решетки соответствует плоскости обратной решетки

10. Основные понятия кристаллохимии: Координационное число и координационный многогранник. Пределы устойчивости структур.

Атом или ион в представление считают несжимаемым наром. Используя планетар-ные модели атома, представляют как ядро с вращающимися электронами. Эффективный атомный радиус - радиус сферы его действия. Сфера радиуса зависит от заполнения электронных оболочек, поэтому атомы в кристаллической структуре представляют как соприкасающиеся шары расстояние между центров которых равно сумме радиусов. Атомные радиусы определяются рентгеновскими методами и вычисляются на основе квантовых представлений. Размеры ионных радиусов подчиняются еще закономернос-тям:

1. Внутри встр. ряда первой системы радиусы ионов с одинаковым зарядом увеличи-вается, так как растет число электронных оболочек.

Fe; Fe²⁺; Fe³⁺

1,26 0,80 0,37 радиус (Å)

Для одного и того же элемента ионный радиус ē увеличивается по мере увеличения отрицательного заряда, и уменьшается по мере увеличения положительного заряда.

Rb^4-; Rb; Rb²⁺ радиус атома больше радиуса катиона

2,15 1,74 1,18

Размеры атомов и ионов следуют периодичной системы элементов(57 - лантан - исключение)

Эффективный радиус иона зависит от номера элемента и от степени его ионизации.

Координационное число и координационное многогранники

Координационное число атома (иона) называется число ближайших однотипных соседних атомов (ионов). Если соединить атомы друг с другом, получится координа-ционный многогранник. Атом для которого строится координационный многогранник должен находиться в центре его. Координационный многогранник не связан с внеш-ней формой кристалла, и не соответствует ей.

В структуре алмаза число соседних ближайших атомов равно 4, многогранник ок-таэдр

NaCl к.ч. = 6 - каждый ион натрия окружен шестью ионами хлора по вершине полей октаэдра.

рис. 1. Структура Сфалерита.

В структуре сфалерита (рис 1) ионы серы окружены ионами цинка, и ионы цинка ок-ружены ионами серы к. ч. = 4 (тетраэдр координационный многогранник)

Пределы устойчивости структур

Относительные размеры атомов и ионов являются основным фактором возникно-вения структур одого вида.

Ионная структура кристалла считается устойчивой, или каждый ион касается про-тивоположно заряженного иона.

Схема иллюстрирует степень устойчивости структур

анионы соприкасаются друг с другом и с катионом. Если уменьшается радиус, струк-тура становится неустойчивой(в,г). Силы отталкивания одноименно заряженных ио-нов вызывают перестройку структуры до более устойчивого состояния с другим ко-ординационным числом. На основание простой геометрической формулы мы можем различить радиусы при которых структура устойчива.

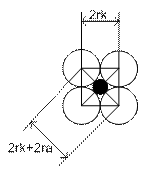
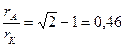
Предельные (минимальные) соотношения радиусов ионов для различных координационных чисел (Таблица Шонгуеа- Гольдшмидта)

Координационное число	Координационный многогранник
	гантель	0 - 0,15
	треугольник	0,15 - 0,22
	тетраэдр	0,22 - 0,41
	октаэдр	0,41 - 0,73
	куб	0,73 - 1,00
	Кубоонтаэдр	> 1,00

Дата добавления: 2015-10-16