Пространственная Решетка кристаллов.

Кристалл - однородное анизотропное тело. Однородность означает, что любые физические свойства кристалла одинаковы во всех его точка. Основная особенность кристаллического состояния заключается в трехмерной периодичности расположения материальных частиц, с учетом дискретного атомного строения кристаллы —вещество, в которых составляющие их частицы (атомы, молекулы) расположена строго периодически, образуя геометрически закономерную кр. структуру Каждое кристаллическое вещество отличается от других кристаллических веществ по его атомной закономерности и симметрии структуры кристаллы однородны и анизотропные. В структурной кристаллографии в понятие однородности учитывающее дискретное. строение кристалла из частиц одного или разных сортов, вкладывается определенный смысл. Кристалл называется однородным, если для любой точки, взятой внутри него, найдется точка, совершенно идентичная по свойствам первой и отстоящая от нее на некотором конечном рас стоянии.)Для кристаллов неорганических веществ, как это следует из экспериментов это расстояние составляет около не скольких нанометров

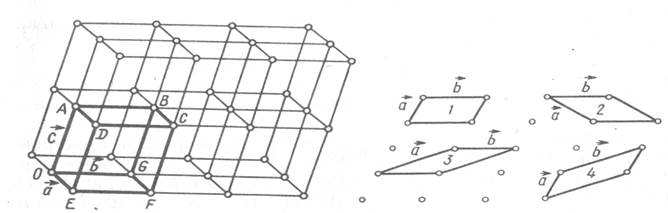
Исходя из определения однородности и учитывая атомную декретную структуру, можно показать, что идентичные точек (в дальнейшем мы будем именовать их узлами, связанные первоначальной, произвольно выбранной точкой тремя некомпланарными векторами переноса, их трансляциями образуют трехмерную периодическую решетку, охватывающую все про ст. кристалла.) Так решетку назвали потому, что идея точные точки кристалла можно соединить трехмерной сеткой из прямых линий, как это показано на рис. 1.2. Следует различать понятия структура кристалла и пространственная решетка. Структура кристалла — это физическая реальность. Когда говорят о структуре кристалла, то имеют в виду конкретное расположение частиц (например, центров масс атомов) в кристаллическом пространстве. Пространственная же решетка, основная роль которой сводится к размножению идентичных точек, не обязательно материальных, является лишь геометрическим построением, помогающим выявить законы сим метрии структуры кристалла.

Решетку можно описать ё помощью периодически повторяющегося в пространстве элементарного параллелепипеда — элементарной ячейки (О, А, В, С, D, Е, F, G на рис. 1.2), по строенной на трех некомпланарных векторах переноса, или единичных трансляциях а, Ь, с, которые могут быть выбраны, во обще говоря, бесчисленным количеством способов (рис. 1.3). Трансляции действуют не на какую-нибудь одну точку решетки, а на всю решетку в целом. Началом трех векторов трансляций можно выбрать любую точку. Если какой-нибудь узел выбранза начало отсчета, то радиус-вектор 1 любого другого узла решетки может быть определен из формулы

Где m, n, р — числа, которые обычно выражают в долях ребер ячейки и называют индексами данного узла. Совокупность трех индексов обычно записывают в двойных квадратных скобках 1 и называют символом узла.

Шесть указанных величин называют параметрами решетки. Параметры а, Ь и с, определяю размер элементарной ячейки, часто называют постоянными решетки.

Углы между соответствующими гранями кристаллов данного вещество постоянны и характерны для этих кристаллов — закон постоянства углов, являющимся проявлением правильного внутреннего атомного строения вещества.

Рис. 7. Иллюстрация закона постоянства углов.

Формула Вульфа—Брэгга. простое истолкование интерференции рентгеновских лучей в кристаллах, объясняется это явление их отражением (как от зеркала) плоскостей. Основываясь на этих соображениях, они вывели формулу, описывающую положение интерференционных макс. Ниже приводит вывод этой формулы, носящей название формулы. Вульфа— Брэгга.

Пусть на кристалл, который можно представить стоящим из семейства параллельных плоскостей, находящихся на межплоскостном расстоянии d (рис. 1.47), под умом θ падает параллельный пучок монохроматических рентгеновских лучей с длиной волны. Отраженные от атомных плоскостей под тем же углом θ (при зеркальном отражении угол падения равен углу отражения, параллельные лучи 1 и II интерферируют, т. е. усиливают или ослабляют друг друга зависимости от разностино хода между ними. Если разность хода Δ= (АВ+ВС)-АD равна целому числу длин волн λ, наблюдается ин максимум. Из рис. 1.47 видно, что это имеет место, когда (1.26)

Условие (1.26), при выполнении которого. возникает интерфе рещионный максимум, и носит незнание формулы Вульфа-Брэгга. Зная брэгговские углы отражения θ, которые определяются из дифракционной картины, можно вычислить межплоскоетные расстояния d, а по. ним и индексы h,k,l.

Дата добавления: 2015-10-16