Метод кристаллографического индицирования.

Для описания кристаллических многогранников и структур применяется метод индицирования. Кристаллическая решетка характеризуется:

1.длинами ребер (а,в,с)

вдоль

где m,n,p- целые

Положение т.М определяется радиус-вектором:

Где - наименьшие векторы трансляции (периоды трансляции)

Символы, индексы узлов.

Если один из узлов принять за начало координат, то другой узел решеткиможно определить радиус-вектором

m,n,p- индексы узла

[[m,n,p]]- символ узла

Индексы направлений (рёбер): Для отыскания направления выбирается прямая, проходящая через начало координат. Её положение однозначно определяется индексами первого узла, через который она проходит.

Индексы граней.

Положение плоскости определяется заданием трёх отрезков А,В,С, которые она отсекает на осях решетки. Выражаются эти отрезки в осевых единицах и записываются величины, обратные этим отрезкам: . Полученные дроби приводят к общему знаменателю (D) и получают величины: ;

Где -h,k,l- индексы плоскости (Миллера)

Получается соотношение:

- уравнение плоскости в общем виде (N- целое, если N=0, то плоскость проходит через начало координат)

Закон целых чисел (Гаюн 1819).

Для двух граней реального кристалла двойные отношения параметров равны отношению целых чисел:

(*), где p,q,r- целые простые, для реальных кристаллов малые числа.

Плоскость A’,B’,C’ может быть гранью кристалла только если отрезки которые она отсекает на осях координат OA’,OB’,OC’ связаны соотношением (*).

На растущем кристалле появляются грани определённого наклона, характерные для данного вещества. Т.о. по закону Гаюна наклон грани кристалла можно определить тремя целыми числами, если за оси координат выбрать направлении 3-х рёбер кристалла, а за единицы измерения выбрать отрезки, отсекающие на этих осях одной из граней кристалла. Закон целых чисел просто истолковывается, если знать, что ребра кристаллов соответствуют рядам решетки, а грани плоскостям сетки. Если за оси координат выбрать ребра, которые соответствуют трём элементам равным трансляциям (рёбрам элементарной ячейки), то двойные отношения отрезков определяют те же символы Миллера (h,k,l), т.е. :

Вывод: Кристаллографическую плоскость и для грань кристалла можно определить тремя целыми числами (индексами Миллера), которые представляют собой:

1. коэффициенты в уравнении плоскости, написаны в параметрической форме

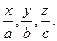
2. величины, обратнопропорциональные отрезкам, отсекаемым плоскостью на осях координат.

3. или величины, пропорциональны двойным отношениям осевых отрезков согласно закону рациональных параметров.

Чтобы построить плоскость (hkl) надо нанести на осях координат отрезки И через полученные точки проходит плоскость семейства hkl ближайшая к началу координат.

Дата добавления: 2015-10-16