Координатные системы. Категории. Сингонии

Необходимость фиксировать то или иное направление (ребро) ту или иную плоскость (грань) заставляет вводить в кристалла координатную систему. Однако пользоваться во всех случаях какой-то единой системой, например наиболее распространенной В аналитической геометрии декартовой, в кристаллографии неудобно, так как прямоугольная система с одинаковыми масштабам по осям не позволит достаточно полно и наглядно отразить си метрию кристаллов. Естественной кристаллографической координатной системой будет такая, в которой координатные оси совмещены с особыми направлениями, т. е. с осями симметрии и нормалями к плоскостям симметрии; при отсутствии или недостаточном числе особых направлений координатные оси совмещают С действительными или возможными ребрами кристалла (если есть одно особое направление с ним вмещают одну координационную ось, а для остальных осей используют лишь такие ребра кристалла, которые лежат в плоскости, перпендикулярной этому на направлению). Следовательно, координатные системы кристаллов будут различаться своими осевыми углами.

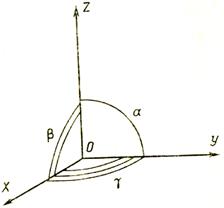Рис. 33. Применяемая в кристаллографии правая система координат

Однако для кристаллографической координатной системы не достаточна лишь угловая характеристика. Так, на рис. 34 представлены три многогранника с ортогональной системой координат, состоящие из равного количества координатных граней (т. е. граней, перпендикулярных координатным осям). однако эти шестигранники существенно отличаются друг от друга:

в Первом случае (рис. 34, б) все грани связаны между собой операциями симметрии трех взаимно перпендикулярных координатных осей 4-го порядка, т. е. составляют одно семейство — одну простую форму. Во втором случае шестерка граней распадается на два семейства — две простые формы: четырехгранную в которой грани параллельны единственной оси высшего порядка (Е и двугранную, состоящую из связанных между собой граней, перпендикулярных L_4. В третьем кристалле (рис. 34, а) отсутствие осей высшего порядка приводит к разбиению шести координатных граней на три независимые двугранные простые формы. Для того чтобы подчеркнуть раз форм этих многогранников, в характеристику их координатных систем необходимо ввести понятие эквивалентности Координатных осей. Нетрудно увидеть, что в первом случае все три координатные оси (L_4х, L_4у, L₄) эквивалентны. Во втором кристалле эквивалентны лишь оси Х и У, тогда как ось Z единственная ось высшего порядка L₄ — оригинальная в третьем кристалле, в котором отсутст ют оси высшего порядка, все три оси координатной системы независимы — неэквивалентны

Таким образом, полная характеристика координатной кристлографической системы должна отразить не только значения осевых углов, но и степень эквивалентности тех направлений, вдоль которых выбраны координатные оси. Такая координатная система отражает не только симметрию кристаллов, но и анизотропию кристаллического вещества.

Дата добавления: 2015-10-16