Политипия

Политипия (или политипизм) — явление, характерное для некоторых плотно упакованных и слоистых структур. Политипы — это структуры, построенные из одних и тех же слоев с разной последовательностью их чередования. Параметры решетки у политипов в плоскости слоя неизменны, а в направ­лении, перпендикулярном слоям, различны, но всегда кратны расстоянию между ближайшими слоями. Различие политипов проявляется и в некоторых их свойствах, особенно в оптических.

Наибольшее богатство политипов обнаружено у карбида кремния SiC, т. е. химического соединения кремния и углерода (А₄В₄) с высокой температурой плавления (более 2000° С). Эти кристаллы обладают ценными полупроводни­ковыми свойствами. Кроме того, карбид кремния вследствие своей исключительно высокой твердости получил широкое распространение в абразивной промышленности. Карбид кремния встречается в кубической модификации типа сфалерита – так называемый β-SiC и в гексагональной модификации α-SiC, структуру которой мы рассмотрим.

Элементарная ячейка гексагонального карбида кремния представлена на рис. 171, а. Это вытянутая продолговатая призма с сечением в виде ромба: вершины заняты атомами 1, 2, 3, 4, 25, 26, 27 и 28. Тупой угол ромба – 120°, так что ромбическую призму можно считать составленной из двух тригональных призм с основаниями в виде равносторонних треугольников.

Для большей наглядности располо­жение ионов углерода в пределах одной элементарной ячейки показано на рис. 171, б, причем указана высота расположения z каждого слоя в долях параметра но оси с. Атомы кремния как бы повторяют закон расположения атомов угле рода: над каждым атомом углерода на одинаковых расстояниях помещается атом кремния. Структура состоит из параллельных равноотстоящих слоев атомов, перпендикулярных оси 6₃.

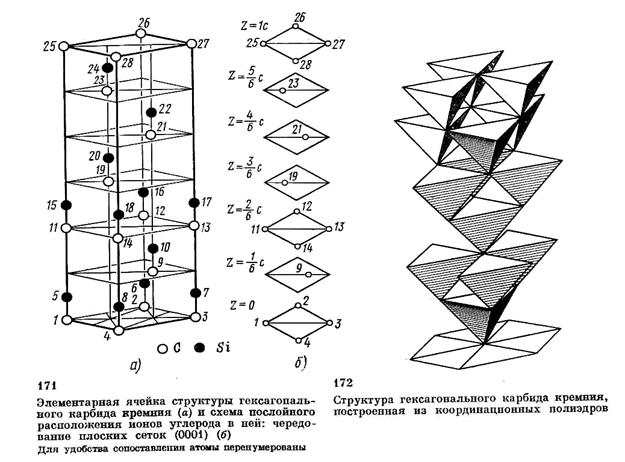
Пространственная группа Р6₃/тс. Вертикальная ось 6₃ проходит по линии центров тяжести правой тригональной призмы. Через большую диагональ элементарной ячейки проходит вертикальная плоскость т., а через малую диагональ — вертикальная плоскость скользящего отражения типа с.

Координационное число углерода по кремнию и кремния по углероду равно 4, к. м. – тетраэдр. К. ч. взятое по атомам того же самого сорта, равно 12, что соответствует плотнейшей упаковке. На одну элементарную ячейку прихо­дится 6 атомов кремния, образующих плотнейшую упаковку, 6 октаэдричесних и 12 тетраэдрических пустот. Атомы углерода занимают 6 тетраэдрических пустот. Все октаэдрические пустоты свободны (рис. 172). Заполненные тетраэдры расположены шестью ярусами, причем среди них нет совпадающих. Упаковка шестислойная с чередованием слоев:

...В АВСАСВ ABC АСЕ АВСАСВ А....

Параметры ячейки: a = b = 3,078 А, с = 2,518 А.

Шестислойная упаковка у карбида кремния наиболее распространена. Кроме нее у этого вещества встречаются политипные модификация, которые представляют собой укладки из таких же слоев, но с другим порядком их чередования, так что параметры ячейки a и b остаются теми же, а параметр с принимает значение пс, где п – период идентичности чередования слоев в структуре. Известны политипы, у которых п = 4, 6, 15, 21, 33, 51 и далее до п = 192, 270, 400, 594 и даже 1200, т. е. с самыми разнообразными чередованиями слоев и с гигантскими элементарными ячейками вплоть до с = 1500 А. У политипа 594 R.

Политипы характеризуются цифрой, указывающей число слоев в элементар­ной ячейке, и буквой, указывающей тип ячейки: пН означает структуру с n-слоеный периодом повторяемости вдоль оси с и примитивной гексагональной ячейкой, a nR – структуру с n-слойным периодом повторяемости вдоль оси с и решеткой, у которой примитивная ячейка ромбоэдрическая (так называемые обозначения Рамсдела).

Шестислойная модификация с чередованием... В АВСАСВ АВСАСВ А... записывается в этих обозначениях как 6Н, ав обозначениях Полинга (см. § 27) как (гкк)₂. Часто встречающаяся четырехслойная модификация с чередованием слоев

... В АВСВ АВСВ...

записывается как 4H или (гк)₂, и так далее вплоть до 70H, 174R, 192R, 594R и даже 1200R; здесь R – ромбоэдрическая ячейка. Для карбида кремния наиболее распространены политипы 6 H, 4 H, а также политип 15 R ≡... В АВСВАСАВАВАСВСАСВ АВСВА САВАСВСАСВ А... (гкгкк)₃.

У кристаллов политипных модификаций несколько различаются и физические свойства, в основном те, которые зависят от параметра решетки по оси с. Так, величина двупреломления света прямо пропорциональна степени усложнения политипа, т. е. параметру пс. Карбид кремния – самый представительный пример полигинии. Для него найдено более 50 иолитипных модификации.

Более десяти политипных модификаций обнаружено у монокристаллов ZnS. Кроме разобранных выше сфалерита (3 C; здесь С – кубическая ячейка) и вюрцита (2 Н)имеются политипы 4 H, 6 H, 8 H, 10 H, 9 R, 12 R, 15 R и др. (рис. 173). Очень часто кристаллы ZnS состоят из набора политипов или сростков разных политипов, которые трудно разграничить.

Полигиния наблюдается в графите, молибдените MoS₂, в кристаллах GdI₂, CdBr₂, РbI₂, в дииодидах переходных элементов титана, ванадия, марганца, железа, цинка, кобальта и др., в дибромидах магния, марганца, железа, кобальта, в соединениях TiS₂, TiSe₂, ZrS₂, SnS₂, PtS₂ и многих других веществах со слоистой структурой.

Дата добавления: 2015-10-16