Дайте определение эллипса Запишите каноническое уравнение и поясните схему построения эллипса.

Определение: Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.

Пусть F ₁ и F ₂ – фокусы эллипса. Начало O системы координат расположим на середине отрезка F ₁ F ₂. Ось Ox направим вдоль этого отрезка, ось Oy – перпендикулярно к этому отрезку (рис.).

Рис. Изображение эллипса по определению

Теорема: Пусть сумма расстояний от точки эллипса до фокусов равна 2 a, а расстояние между фокусами – 2c. Тогда в выбранной системе координат эллипс имеет уравнение , где b ² = a ² – c ².

Доказательство. Пусть M (x; y) – текущая точка эллипса. По определению эллипса F ₁ M + F ₂ M = 2 a. Из треугольника F ₁ MF ₂ (рис. 13) видно, что F ₁ M + F ₂ M > F ₁ F ₂, то есть 2 a >2 c, a > c, и поэтому число b ² = a ² – c ² существует.

Фокусами в выбранной системе координат являются точки F ₁(- c;0), F ₂(c;0). По формуле расстояния для плоского случая находим 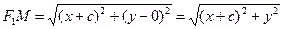, 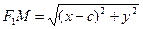. Тогда по определению эллипса .

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению .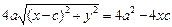

Разделим обе части этого уравнения на 4 и возведем в квадрат a ²(x ² – 2 xc + c ² + y ²) =a⁴ – 2 a ² xc + x ² c ².

Раскроем скобку и приведем подобные члены x ²(a ² – c ²) + a ² y ² = a ²(a ² – c ²).

Учитывая, что b ² = a ² – c ², имеем равенство x ² b ² + y ² a ²= a ² b ².

Наконец, разделив обе части на a ² b ², получим уравнение .

Уравнение называется каноническим уравнением эллипса.

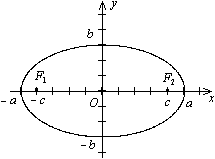
Рис.Эллипс

Определение: Точки пересечения эллипса с его осями симметрии называются вершинами эллипс а, центр симметрии – центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины – большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины – малой полуосью. Величина 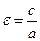называется эксцентриситетом эллипса.

Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (– a;0), (a;0),(0; – b), (0; b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы c ² = a ² – b ².

Эксцентриситет эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0< <1.

8. Какая линия на плоскости называется гиперболой? Запишите каноническое уравнение и поясните схему построения гиперболы.

Определение: Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.

Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось Ox направим вдоль этого отрезка, а ось ординат – перпендикулярно к нему.

Теорема: Пусть расстояние между фокусами F ₁ и F ₂ гиперболы равно 2 c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2 a. Тогда гипербола в выбранной выше системе координат имеет уравнение , где b ² = c ² – a ²

Доказательство. Пусть M (x; y) – текущая точка гиперболы (рис.).

Рис. Изображение гиперболы по определению

Так как разность двух сторон треугольника меньше третьей стороны, то , то есть 2 a <2 c, a < c. В силу последнего неравенства вещественное число b существует.

По условию, фокусы – F ₁(– c;0), F ₂(c;0). По формуле вычисления расстояния между точками для случая плоскости получаем

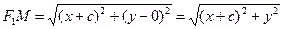
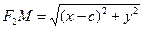
По определению гиперболы

.

Это уравнение запишем в виде

.

Обе части возведем в квадрат:

После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

a ²(x ² – 2 xc + c ² + y ²) = x ² c ² – 2 a ² xc + a ⁴.

Раскрывая скобку и приводя подобные члены, получим

x ²(c ² – a ²) – a ² y ² = a ²(c ² – a ²).

С учетом формулы b ² = c ² – a ² уравнение принимает вид x ² b ² – y ² a ²= a ² b ²

Разделим обе части уравнения на a ² b ² и получим уравнение . Уравнение называется каноническим уравнением гиперболы.

Предложение: Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси Ox и Oy, а начало координат – центр симметрии гиперболы.

Проведем построение гиперболы:

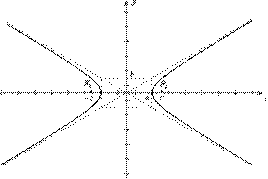
Рис. 7. Гипербола

Определение: Точки пересечения гиперболы, заданной каноническим уравнением с осью Ox называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0;– b) и (0; b) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 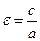называется эксцентриситетом гиперболы.

Замечание: Из равенства b ² = c ² – a ² следует, что c > a, то есть у гиперболы >1. Эксцентриситет характеризует угол между асимптотами, чем ближе к 1, тем меньше этот угол.

9. Какая линия на плоскости называется параболой? Запишите каноническое уравнение параболы. Поясните схему построения параболы.

Определение: Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса F опустим перпендикуляр FD на директрису l. Начало координат O расположим на середине отрезка FD, ось Ox направим вдоль отрезка FD так, чтобы ее направление совпадало с направлением вектора . Ось Oy проведем перпендикулярно оси Ox (рис.).

Рис. Изображение параболы по определению

Теорема: Пусть расстояние между фокусом F и директрисой l параболы равно p. Тогда в выбранной системе координат парабола имеет уравнение y ² = 2 px

Доказательство. В выбранной системе координат фокусом параболы служит точка F (), а директриса имеет уравнение .

Пусть M (x; y) – текущая точка параболы. Тогда по формуле вычисления расстояния для плоского случая находим

Расстоянием от точки M до директрисы l служит длина перпендикуляра MK, опущенного на директрису из точки M. Из рисунка 8 очевидно, что . Тогда по определению параболы MK = FM, то есть .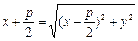

Возведем обе части последнего уравнения в квадрат: 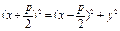, откуда .

После приведения подобных членов получим уравнение y ² = 2 px. Уравнение называется каноническим уравнением параболы.

Предложение: Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью Ox.

Точка пересечения оси симметрии с параболой называется вершиной параболы.

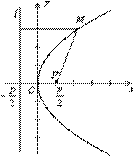
Рис. Парабола

Дата добавления: 2015-10-16