Расскажите об основных типах матричных уравнений и схемах их решения.

Понятие обратной матрицы дает возможность решать матричные уравнения. Пусть имеется уравнение вида , где , , 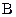, - некоторые матрицы, причем - неизвестная. Для нахождения , прежде всего, необходимо 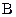перенести вправо: 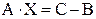. Затем, пользуясь тем, что , умножим равенство на :

.

При решении подобных уравнений необходимо учитывать, с какой стороны стоит множитель при . Если уравнение имеет вид , то

.

Если же уравнение имеет множители при с обеих сторон

(), то .

9. Дать определение решения системы линейных уравнений. Расшифруйте понятия «совместная», «несовместная», «определенная», «неопределенная» системы.

Определение1. Системой m линейных уравнений с n неизвестными называется система S вида

,

где коэффициенты при неизвестных, свободные члены ( , заданные числа).

Определение 2. Решением системы называется упорядоченный набор действительных чисел , при подстановке которых в каждое уравнение системы вместо соответственно будут получены верные числовые равенства.

Определение 3. Система называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений).

Определение 4. Совместная система линейных алгебраических уравнений называется определённой (неопределённой), если она имеет единственное решение (множество решений).

Определение 5. Матрица , составленная из коэффициентов при неизвестных, называется основной матрицей системы :

Матрица

называется расширенной матрицей этой системы.

Замечание. Система может быть переписана в так называемом матричном виде:

где вектор-столбец свободных членов системы.

10. Напишите формулы Крамера. В каком случае они применимы?

Данный метод применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:

Теорема 5.2. Система линейных уравнений с неизвестными

основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам

где определитель матрицы, полученной из основной матрицы системы уравнений заменой её 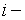го столбца столбцом свободных членов.

11. В чем заключается матричный метод решения систем? Когда он применим?

Данный метод применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений.

Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A^-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A^-1B называют матричным способом решения системы, или решением по методу обратной матрицы.

12. Что следует из равенства нулю определителя системы?

Если определитель системы равен нулю, то система не имеет решения.

13. Что называется рангом матрицы? Как он находится?

Рассмотрим прямоугольную матрицу

A =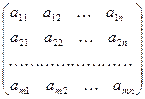

Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель этой матрицы называется минором k -го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r (A). Очевидно, что выполняется соотношение 0 ≤ r (A) ≤ min (m, n).

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k -го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k +1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так:

A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю,

например, .

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

---

Дата добавления: 2015-10-16