Изложите схему приведения общего уравнения кривой к каноническому виду.

Привести кривую второго порядка

(1)

к каноническому виду.

План решения.

Инварианты относительно переноса начала координат и поворота осей:

.

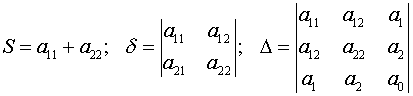Полуинвариант уравнения (1) (инвариант относительно поворота осей):

.

В зависимости от значений величин уравнение (1) определяет одну из следующих линий:

			действительный эллипс
	мнимый эллипс
	пара мнимых сопряженных пересекающихся прямых
		гипербола
	пара действительных пересекающихся прямых
		парабола
		пара мнимых параллельных прямых
	пара действительных параллельных прямых
	пара действительных совпадающих прямых

11. Дайте понятие полярной системы координат. Уравнения линий в полярной системе координат. Приведите примеры. Как связаны декартовы и полярные координаты точки на плоскости? Как построить кривую в полярной системе координат?

Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел (ρ; φ). Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось. Координата ρ – расстояние от точки до полюса, координата φ – угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку, который берется со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «–» в противоположном случае. Важно понимать, что число φ в полярной системе определено не однозначно: парам чисел (ρ; φ + 2π n) соответствует одна и та же точка при любых натуральных n. Для полюса ρ = 0, а угол φ не определен.

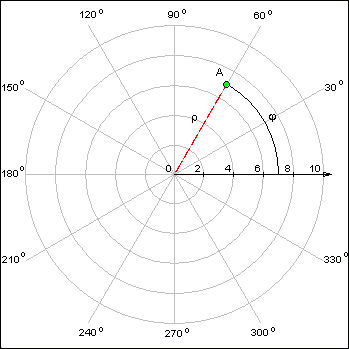
Рис1. Полярная система координат.

Полярные координаты легко преобразовать в декартовы. Пусть (x; y) – координаты точки в декартовой системе координат, (ρ; φ) – в полярной. Тогда очевидно, что

Формулы обратного перехода:

Если же известны прямоугольные координаты и точки, ее полярные координаты определяются по формулам

; ; ;

Дата добавления: 2015-10-16