Таким образом, однородная система линейных уравнений всегда совместна. Поэтому важно выяснить, при каких условиях она является определенной.

В самом деле, пусть D = 0. Так как однородная система уравнений является частным случаем неоднородной системы, то к ней применимо правило Крамера. Но для однородной системы все Dx_i = 0, так как каждый из этих определителей содержит столбец из нулей (b_i = 0). Поэтому система, равносильная системе (3), будет иметь вид

D_x1= 0, D_x2=0;...,D_xn= 0

Из этой системы следует, что однородная система имеет единственное нулевое решение, если Δ 0; если же D = 0, то она имеет бесчисленное множество решений.

Векторная алгебра

1. Что называется вектором, модулем вектора?

Определение 1: Вектором называется направленный отрезок.

Таким образом, вектор – это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора.

Определение 2: Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается׀ a ׀. Вектор a называется единичным, если ׀ a ׀=1.

Дайте понятие коллинеарных, компланарных, свободных, равных векторов. Сформулируйте условие равенства векторов.

Определение 1: Два вектора называются равными, то есть не различаются как векторы, если соответствующие отрезки параллельны, имеют одинаковую длину и направление.

Если считать, что на рисунке 1 векторы лежат в одной плоскости, то а = с, то есть a и c – разные обозначения одного и того же вектора. Векторы a и при равных длинах не равны друг другу, так как имеют разные направления. В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится.

Определение 2: Векторы называются коллинеарными, если они параллельны одной прямой.

Определение 3: Векторы называются компланарными, если они параллельны одной плоскости.

Свободный вектор – вектор, который вполне определен своими координатами: он не привязан ни к какой точке пространства и при параллельном переносе (с сохранением направления и длины) его координаты не изменяются. Если вектор задан в координатной форме, то никто не скажет, где он расположен.

Условие равенства векторов: 2 вектора равны, если они имеют одинаковую длину и направлены в одну сторону.

3. Как выполняются линейные операции над векторами? Каковы свойства этих операций?

Определение 1: Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c – его диагональ.

Определение 2: Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и׀ a ׀=׀ b ׀.

Вектор, противоположный вектору a, обозначается – а, то есть .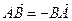

Определение 3: Разностью векторов a и b называется сумма а + (– b).

Разность обозначается a – b, то есть a – b= а + (– b)..

Определение 4: Произведением вектора a на вещественное число называется вектор b, определяемый условием

1) ׀ b ׀ = ׀ ׀·׀ a ׀ и, если ׀ b ׀ 0, то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если >0, и противоположно, если <0.

Произведение вектора a на число обозначается a

Теорема 1: Для любых векторов a, b, c и любых вещественных чисел выполняются следующие свойства:

1) a + b = b + a (свойство коммутативности операции сложения);

2) (a + b) + c = a + (b + c) (свойство ассоциативности операции сложения);

3) a + 0 = a;

4) a + (– a) = 0;

5) ( a) = ( ) a (свойство ассоциативности по отношению к числам);

6) (a + b) = a + b (свойство дистрибутивности по отношению к умножению на число);

7) ( + ) a = a + a (свойство дистрибутивности по отношению к умножению на вектор;

8) 1· a = a.

Сформулируем еще несколько очевидных свойств операций сложения и умножения вектора на число:

9) равенство a =0 верно тогда и только тогда, когда или =0 или a =0;

10) вектор, противоположный вектору a, равен (–1)· a, то есть – a = (–1)· a;

11) для любых векторов a и b существует такой вектор x, что a + x = b.

4. Какие векторы называются линейно зависимыми и независимыми?

Определение 1: Система векторов a ₁, a ₂,…, a _k называется линейно зависимой, если существует такой набор коэффициентов ₁, ₂,…, _k, из которых хотя бы один отличен от нуля, что ₁ a ₁ + ₂ a ₂ +… + _k a _k = 0.

Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по-другому.

Определение 2: Система векторов a ₁, a ₂,…, a _k называется линейно независимой, если равенство ₁ a ₁ + ₂ a ₂ +… + _k a _k = 0 возможно только при ₁= ₂=…= _k.

5. Дайте понятие базиса на прямой, плоскости и в пространстве. Что такое координаты вектора?

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Координатами (или компонентами) вектора a в базисе e ₁,… e ₃ называются коэффициенты разложения вектора a по векторам базиса.

Для указания, что вектор a имеет координаты ₁,…, ₃, мы будем использовать запись a = ( ₁,…, ₃).

Очевидно, что в фиксированном базисе каждый вектор имеет свой, единственный, набор координат. Если же взять другой базис, то координаты вектора в общем случае изменятся.

6. Какой базис называется декартовым? Как осуществляются линейные операции над векторами в координатной форме?

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор 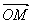назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.

1-я ось – ось абсцисс

2-я ось – ось ординат

3-я ось – ось апликат

В связи с этим можно записать следующие свойства:

-равные векторы имеют одинаковые координаты,

-при умножении вектора на число его компоненты тоже умножаются на это число,

-при сложении векторов складываются их соответствующие компоненты.

---

Дата добавления: 2015-10-16