
Читайте также:
|
Ортом вектора называется вектор единичной длины, имеющий то же направление, что и вектор
Косинусы углов, образованных вектором с осями координат, называются направляющими косинусами вектора.

В соответствии с рисунком, направляющими косинусами вектора a являются cos  , cos
, cos 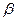 , cos
, cos 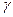 .
.
Предложение: Координаты вектора равны его направляющим косинусам, умноженным на длину вектора. Если вектор единичный, то его координатами служат направляющие косинусы.
9. Что называется скалярным произведением двух векторов? Каковы его свойства? Как выражается скалярное произведение через координаты перемножаемых векторов? Для решения каких задач и как может быть использовано скалярное произведение?
Определение 1: Скалярным произведением векторов a и b называется число, равное ׀ a ׀ ׀ b ׀ cos 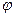 , где
, где 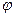 – угол между векторами a и b.
– угол между векторами a и b.
Скалярное произведение обозначается a · b или ab или (a, b). Скалярное произведение вектора на себя, aa, обозначается a 2. Скалярное произведение обладает следующими свойствами, которые мы сформулируем в виде теоремы.
Теорема 1: Для любых векторов a и b выполнены следующие соотношения:
1) ab = ba, свойство коммутативности;
2) a (b + c) = ab + ac, свойство дистрибутивности;
3)(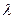 a) b =
a) b = 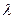 (ab);
(ab);
4) a 2>0 при a  0;
0;
5) a 2 = ׀ a ׀2;
6) Если 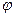 – угол между векторами a и b, то
– угол между векторами a и b, то 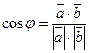 ;
;
7) ab= ׀ a ׀Пр ab, если a  0;
0;
8) ab =0 тогда и только тогда, когда векторы a и b ортогональны.
Теорема 2: Если векторы в ортонормированном базисе заданы своими координатами a ( 1,
1,  2,
2,  3), b (
3), b (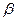 1,
1, 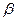 2,
2, 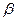 3), то ab =
3), то ab =  1
1 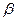 1+
1+  2
2 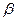 2+
2+  3
3 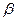 3
3
10. Что называется векторным произведением двух векторов? Каковы его свойства? Как выражается векторное произведение через координаты перемножаемых векторов? Для решения каких задач и как может быть использовано векторное произведение?
Определение 1: Векторным произведением вектора a на вектор b назовем вектор c, удовлетворяющий условию
1) ׀ c ׀ = ׀ a ׀ ׀ b ׀ sin 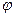 , где
, где 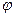 – угол между a и b и, если ׀ c ׀
– угол между a и b и, если ׀ c ׀  0, то еще двум условиям:
0, то еще двум условиям:
2) вектор c ортогонален векторам a и b;
3) из конца вектора c кратчайший поворот от вектора a (первого сомножителя) к вектору b (второму сомножителю) виден против часовой стрелки. (Начала векторов предполагаются совмещенными).
Замечание 1: Угол между векторами в пространстве всегда удовлетворяет условию 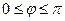 . Таким образом, sin
. Таким образом, sin 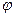
 . Если a =0 или b =0, то считается, что векторное произведение равно 0.
. Если a =0 или b =0, то считается, что векторное произведение равно 0.
Векторное произведение вектора a на вектор b обозначается a × b или [ a, b ].
Предложение 1: Векторное произведение антикоммутативно, то есть a × b = – b × a.
Предложение 2: Векторное произведение a × b равно нулю тогда и только тогда, когда векторы a и b – коллинеарные.
Предложение 3: Для любых векторов a и b и любого числа 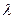 выполняется равенство (
выполняется равенство (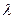 a)× b =
a)× b = 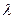 (a × b).
(a × b).
Предложение 4: Векторное произведение обладает свойством дистрибутивности, то есть a ×(b + c) = a × b + a × c.
С помощью векторного произведения можно найти площади параллелограмма и треугольника.
Предложение 5: Площадь параллелограмма, сторонами которого служат векторы a и b, равна модулю их векторного произведения, S пар = ׀ a × b ׀
Площадь треугольника со сторонами a, b вычисляется по формуле  =
= 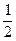 ׀ a × b ׀.
׀ a × b ׀.
Отметим еще одну особенность векторного произведения, отличающую его от операции умножения чисел.
Предложение 6: Векторное произведение не является ассоциативным, то есть существуют такие векторы a, b, c, что (a × b)× c = a ×(b × c).
11. Что называется смешанным произведением двух векторов? Каковы его свойства? Как выражается смешанное произведение через координаты перемножаемых векторов? Для решения каких задач и как может быть использовано смешанное произведение?
Определение 1: Смешанным произведением векторов a, b, c называется число a ·(b 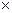 c).
c).
Смешанное произведение будем обозначать abc.
Предложение 1: Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a, b, c компланарны.
Следующее предложение показывает геометрический смысл смешанного произведения.
Предложение 2: Смешанное произведение abc некомпланарных векторов равно объему параллелепипеда, сторонами которого служат векторы a, b, c, взятому со знаком «+», если векторы образуют правую тройку, и со знаком «-», если - левую.
Заметим, что если тройка векторов a, b, c является правой, то тройки c, a, b и b, c, a также будут правыми, а тройки b, a, c, c, b, a и a, c, b будут левыми тройками векторов.
Так как объем параллелепипеда не зависит от того, в каком порядке перечисляются его стороны, то abc = cab = bca =- bac =- cba =- acb.
Предложение 3: Смешанное произведение линейно по каждому аргументу.
Линейность операции по какому-то аргументу означает выполнение двух условий:
1) если аргумент умножить на число, то и результат умножится на это число, то есть числовой множитель аргумента можно вынести за знак операции;
2) если аргумент заменить суммой двух слагаемых, то результат будет равен сумме результатов для каждого слагаемого.
В частности, утверждение, что смешанное произведение линейно по второму аргументу, означает:
1) a (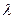 b) c =
b) c = 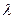 (abc);
(abc);
2) a (b 1 + b 2) = ab 1 c + ab 2 c.
Предложение 4: Объем треугольной пирамиды, ребрами которой служат векторы a, b, c, равен 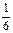 ׀ abc ׀.
׀ abc ׀.

Предложение 5: Пусть в правом ортонормированном базисе i, j, k заданы векторы a ( 1,
1,  2,
2,  3), b (
3), b (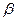 1,
1, 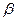 2,
2, 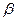 3) c (
3) c (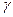 1,
1, 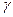 2,
2, 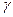 3). Тогда abc =
3). Тогда abc = 
Запишите в векторной и координатной формах условия коллинеарности, перпендикулярности и компланарности векторов.
Условие коллинеарности двух векторов в координатной форме.
Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если  , то
, то 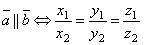 .
.
Дата добавления: 2015-10-16; просмотров: 202 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Таким образом, однородная система линейных уравнений всегда совместна. Поэтому важно выяснить, при каких условиях она является определенной. | | | Запишите различные виды уравнений прямой на плоскости и укажите геометрический смысл параметров уравнений. |