Что такое матрица, отличие матрицы от определителей. Перечислите и приведите примеры различных видов матриц.

При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = n – ее порядком.

В дальнейшем для записи матриц будут применяться либо сдвоенные черточки, либо круглые скобки:

или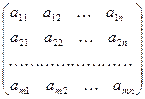

Для краткого обозначения матрицы часто будет использоваться либо одна большая латинская буква (например, A), либо символ || a _ij ||, а иногда с разъяснением: А = || a _ij || = (a _ij ), где (i = 1, 2,..., т, j=1, 2,..., n).

Числа a _ij , входящие в состав данной матрицы, называются ее элементами. В записи a _ij первый индекс і означает номер строки, а второй индекс j – номер столбца. В случае квадратной матрицы

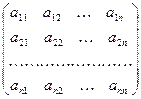
вводятся понятия главной и побочной диагоналей. Главной диагональю матрицы (1.1) называется диагональ а₁₁ а₁₂ … a_nn идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называется диагональ а_n1 а_(n-1)2 … a_1n , идущая из левого нижнего угла в правый верхний угол.

Отличие матриц от определителей: матрица – это таблица, определитель – это число.

Определители существуют только для матриц квадратного вида, ибо для матриц другого типа не существует определителей.

Виды матриц

Если m = n, то матрица называется квадратной матрицей порядка n.

Матрица размера m ×1 называется матрицей-столбцом.

.

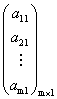Матрица размера n ×1 называется матрицей-строкой.

.

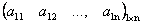Определение 1. Элементы матрицы, имеющие равные индексы, образуют главную диагональ матрицы.

Определение 2. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.

Определение 3. Диагональная матрица n -го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n -го порядка и обозначается Е.

Определение 4. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю.

5. Как осуществляются линейные операции над матрицами?

Сложение матриц: Суммой двух матриц, например: A и B, имеющих одинаковое количество строк и столбцов, иными словами, одних и тех же порядков m и n называется матрица С = (С_ij)(i = 1, 2, …m; j = 1, 2, …n) тех же порядков m и n, элементы C_ij которой равны.

C_ij = A_ij + B_ij (i = 1, 2, …, m; j = 1, 2, …, n)

Для обозначения суммы двух матриц используется запись C = A + B. Операция составления суммы матриц называется их сложением.

Итак, по определению имеем:

+ =

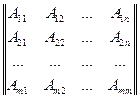Из определения суммы матриц непосредственно вытекает, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно:

1) переместительным свойством: A + B = B + A

2) сочетательным свойством: (A + B) + C = A + (B + C)

Эти свойства позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.

Умножение матрицы на число:

Произведением матрицы A = (A_ij) (i = 1, 2, …, m; j = 1, 2, …, n) на вещественное число называется матрица C = (C_ij) (i = 1, 2, …, m; j = 1, 2, …, n), элементы которой равны

C_ij = A_ij (i = 1, 2, …, m; j = 1, 2, …, n).

Для обозначения произведения матрицы на число используется запись C = A или C = A . Операция составления произведения матрицы на число называется умножением матрицы на это число.

Умножение матрицы на число обладает следующими свойствами:

1) распределительным свойством относительно суммы матриц: (A + B) = A + B

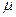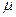2) сочетательным свойством относительно числового множителя: ( )A = ( A)

3) распределительным свойством относительно суммы чисел: ( + 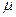) A 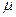= A + A.

Замечание: Разностью двух матриц A иB одинаковых порядков естественно назвать такую матрицу C тех же порядков, которая в сумме с матрицей B дает матрицу A. Для обозначения разности двух матриц используется естественная запись: C = A – B.

6. Как перемножить две матрицы? Сформулируйте правило умножения матрицы на матрицу. Свойства произведения матриц.

Произведением матрицы A = (A_ij) (i = 1, 2, …, m; j = 1, 2, …, n), имеющей порядки соответственно равные m и n, на матрицу B = (B_ij) (i = 1, 2, …, n; j = 1, 2, …, p), имеющую порядки соответственно равные n и p, называется матрица C = (С_ij) (i = 1, 2, …, m; j = 1, 2, …, p), имеющая порядки, соответственно равные m и p, и элементы C_ij, определяемые формулой:

Cij = 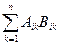(i = 1, 2, …, m; j = 1, 2, …, p))

Для обозначения произведения матрицы A на матрицу B используют запись C = AB. Операция составления произведения матрицы A на матрицу B называется перемножением этих матриц. Из сформулированного выше определения вытекает, чтоматрицу A можно умножить не на всякую матрицу B: необходимо чтобы число столбцов матрицы A было равно числу строк матрицы B. Для того чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.

Формула представляет собой правило составления элементов матрицы C, являющейся произведением матрицы A на матрицу B. Это правило можно сформулировать и словесно: Элемент C_ij, стоящий на пересечении i-й строки и j-го столбца матрицы C = AB, равен сумме попарных произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы B. В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц второго порядка

· =

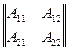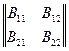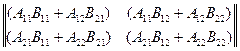
Из формулы вытекают следующие свойства произведения матрицы A на матрицу B:

1) сочетательное свойство :(AB) C = A (BC);

2) распределительное относительно суммы матриц свойство: (A + B) C = AC + BC или A (B + C) = AB + AC.

Вопрос о перестановочном свойстве произведения матриц имеет смысл ставить лишь для квадратных матриц одинакового порядка. Элементарные примеры показывают, что произведений двух квадратных матриц одинакового порядка не обладает, вообще говоря, перестановочным свойством. В самом деле, если положить

A = 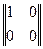, B = 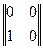, то AB = 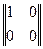, а BA =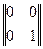

Те же матрицы, для произведения которых справедливо перестановочное свойство, принято называть коммутативным.

Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Среди всех диагональных матриц с совпадающими элементами на главной диагонали особо важную роль играют две матрицы. Первая из этих матриц получается, когда все элементы главной диагонали равны единице, называется единичной матрицей n-ого порядка и обозначается символом E. Вторая матрица получается при всех элементах равных нулю и называется нулевой матрицей n-ого порядка и обозначается символом O. Допустим, что существует произвольная матрица A, тогда

AE = EA = A, AO = OA = O.

7. Изложите схему нахождения обратной матрицы. Любая ли матрица имеет обратную? Что такое вырожденная матрица?

Рассмотрим квадратную матрицу

А =

Обозначим Δ = det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение АВ = ВА = Е, где Е ‑ единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А ^-1, так что В = А ^-1. Обратная матрица вычисляется по формуле

А ^-1 = 1/Δ ,

где А _ij - алгебраические дополнения элементов a _ij.

Вычисление обратной матрицы по формуле приведенной выше, для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Дата добавления: 2015-10-16