Плоскость, ее общее уравнение.

Постановка задачи. Даны точка М₀(х₀ ,у₀ ,z₀ ) и вектор (A,B, С). Написать уравнение плоскости, проходящей через точку М_о, перпендикулярно вектору .

М(х, у, z) - текущая точка плоскости. Точка М принадлежит искомой плоскости тогда и только тогда, когда вектор то есть, когда скалярное произведение векторов

или в координатной форме

А(x-y₀)+B(y-y₀)+C(z-z₀)=0.

Полученное уравнение является уравнением плоскости, проходящей через точку М₀(х₀ ,у₀ ,z₀ ) перпендикулярно вектору (A,B,C).

Вектор называется нормальным вектором плоскости. Если в последнем уравнении приведем подобные члены, то получим общее уравнение плоскости:

Ax+By+Cz+D=0.

Уравнение плоскости в отрезках:

Используя условие компланарности трех векторов, можно записать уравнение плоскости, проходящей через точку M₀ и параллельную векторам и

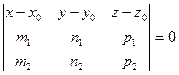
Уравнение плоскости, проходящей через три точки, имеет вид

2. Как определяется взаимное расположение плоскостей? Запишите формулы для определения угла между плоскостями, условия параллельности и перпендикулярности плоскостей.

Углом между плоскостями в пространстве называется угол между нормальными векторами этих плоскостей. Две плоскости и заданы уравнениями и , где , .

Наименьший из двух смежных углов, образованных этими плоскостями, находится по формуле:

Условие параллельности плоскостей:

Две плоскости параллельны тогда и только тогда, когда их нормальные вектора коллинеарны, т.е.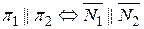

Условие перпендикулярности плоскостей:

Две плоскости перпендикулярны тогда и только тогда, когда их нормальные вектора перпендикулярны, т.е.

Условие совпадения двух плоскостей :

3. Выведите формулу для вычисления расстояния от точки до плоскости. Как определить расстояние между параллельными плоскостями?

Расстояние от точки до плоскости находится по формуле

Дата добавления: 2015-10-16