Внутренне- и внешне устойчивые множества вершин

Дадим определения сразу для неориентированного и ориентированного случаев, учиты-вая, что эти определения очень похожи (отличия будем указывать в скобках). Две различные вершины, которые соединены ребром (дугой), т.е. являющиеся концами одного и того же ребра (дуги), называются смежными. В противном случае две вершины не смежны. Множество X вершин графа G, любые две из которых не смежны, называется внутренне устойчивым, а мак- симально возможное число элементов внутренне устойчивого множества − числом внутренней устойчивости графа G. Число вершин, смежных любой вершине графа, называется степенью данной вершины.

Множество X вершин графа G называется внешне устойчивым, если любая вершина из V – X, т.е. вершина, не принадлежащая X, смежна хотя бы с одной вершиной из X (является кон-цом некоторой дуги, начало которой принадлежит множеству вершин X). Минимально возмож-ное число элементов внешне устойчивого множества называется числом внешней устойчивос-ти графа G (обозначается β (G)).

Множество X вершин графа G, одновременно внутренне и внешне устойчивое, называет-ся ядром графа G.

Заметим, что определения внутренне устойчивого множества вершин в обоих случаях сов-падают. Совпадают и определение ядра. Отличаются только определения внешне устойчивого

множества: в ориентированном случае требуется, чтобы дуга, соединяющая множества X и V – X, имела направление от X к V – X. Содержательный смысл такого понятия будет прояснён в разделе 5.2.

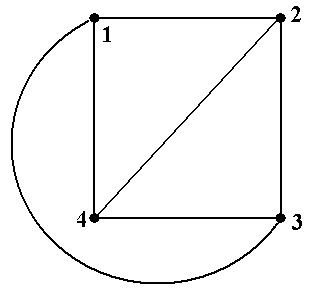
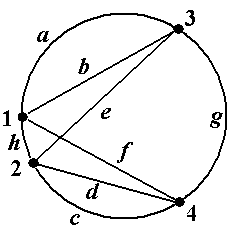
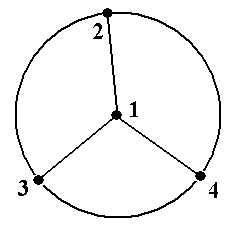
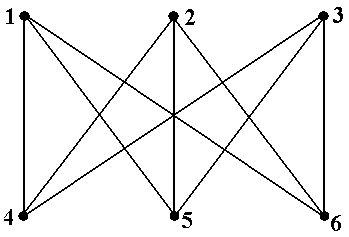
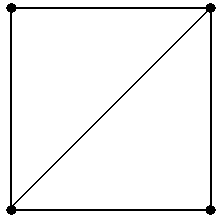
Рис.5.

Обратим внимание на следующее. По приведённым выше определениям, любое одноэле-ментное множество вершин является внутренне устойчивым в силу «ложности посылки»: дейс-твительно, в этом множестве упоминаемые в определении «любые две вершины» просто отсут-ствуют из-за того, что рассматриваемое множество одноэлементно. Множество V всех вершин графа является в силу «ложности посылки» внешне устойчивым: упоминаемая в определении «любая не принадлежащая V вершина» не существует именно потому, что V – это множество всех вершин графа. Из определений внутренней и внешней устойчивости непосредственно сле-дует, что:

- любая изолированная вершина графа может быть добавлена к любому не содержащему её внутренне устойчивому множеству и это расширенное множество также будет внутренне устойчивым;

- любое внешне устойчивое множество обязано содержать любую изолированную верши-ну.

Сформулируем утверждения, относящихся к введённым понятиям.

Утверждение 1. Любое подмножество внутренне устойчивого множества внутренне ус-тойчиво ■

Утверждение 2. Любое множество, содержащее внешне устойчивое множество, внешне устойчиво ■

Утверждение 3. Пусть в некотором графе G X – внешне устойчивое множество, Y –внутреннеустойчивое множество, и

X Z Y. (3)

Тогда Z – ядро графа G ■

Простым следствием из утверждения 3 является следующее

Утверждение 4. Пусть Z – ядро в некотором графе G. Тогда существуют минимальное по включению внешне устойчивое множество X и максимальное по включению внутреннеустой-чивое множество Y, для которых выполнены включения (3) ■

Заметим, что все четыре утверждения верны как в неориентированном, так и в ориентиро-ванном случаях. Однако следующее утверждение верно только для неориентированных графов.

Утверждение 5. Любое максимальное по включению (т.е. не содержащееся ни в каком другом) внутренне устойчивое множество является и внешне устойчивым, т.е. является ядром ■

Поскольку в любом неориентированном графе (как и в любом ориентированном) множес-тво, состоящее из одной вершины, является внутренне устойчивым, то существует и макси-мальное по включению внутренне устойчивое множество. А оно, в силу утверждения 5, являет-ся ядром.

Утверждение 5 даёт гарантию существования ядра для неориентированных графов. А простой пример отсутствия ядра в орграфе даётся ниже.

Пример 7. Проиллюстрируем понятия внутренне и внешне устойчивых множеств вершин в неориентированном графе. Для этого рассмотрим граф, показанный на рис.6 (см. также рис. 1 a). В графе на рис.6 двухэлементные множества вершин {1, 3}, {3, 5} и одноэлементные мно-жества вершин {2}, {4} являются максимальными по включению внутренне устойчивыми мно-жествами. Ясно, что внутренне устойчивые множества {1}, {3} и {5} не являются максималь-ными по включению (они содержатся в {1, 3} или {3, 5}), а любое множество, состоящее из трёх или более вершин, в данном графе внутренне устойчивым не является (проверьте!). Поэто-му число внутренней устойчивости α (G) данного графа G равно 2. Никакие двухэлементные множества, кроме {1, 3} и {3, 5}, внутренне устойчивыми не являются (проверьте!). А все одно-элементные множества вершин внешне устойчивы в любом графе и, значит, в данном.

Минимальными по включению внешне устойчивыми множествами вершин являются те же самые множества вершин {2}, {4}, {1, 3}, {3, 5}, так как другие одноэлементные множества внешне устойчивыми не являются, а все двухэлементные множества, не содержащие подмно-жеств {2} или {4}, совпадают с одним из множеств {1, 3} или {3, 5}. Наконец, все трёх-, четы-рёх- и пятиэлементные множества вершин содержат одно из этих же четырёх множеств: {2}, {4}, {1, 3}, {3, 5}.

Таким образом, каждое из указанных 4-ёх множеств является одновременно внутренне- и внешне устойчивым и, значит, по определению является ядром. Других ядер в данном графе нет ■

Задание 2а. Вграфах, показанных на рис.5, найти все максимальные по включению внут- ренне устойчивые множества вершин, все минимальные по включению внешне устойчивые

множества вершин и все ядра ■

Рис.6

Задание 2b. Вграфах, показанные на рис.7, найти два ядра с разным числом вершин или установить отсутствие таких ядер ■

Пример 8. На рис.8 показан орграф из примера 6 (сеть питания) с пронумерованными вер-шинами 1 – 5. В этом орграфе внутренне устойчивыми множествами являются все одноэлемен-

тные множества {1}, {2}, {3}, {4}, {5} и двухэлементные множества {1, 3}, {1, 4}, {2, 4}, {4, 5}. Других внутренне устойчивых множеств в данном орграфе нет.

Одноэлементных внешне устойчивых множеств в данном случае нет (так как нет ни одной вершины, откуда дуги ведут во все остальные). Единственным двухэлементным внешне устой-чивым множеством является {1, 4} (так как дуги á1, 5ñ, á1, 2ñ и á4, 3ñ ведут из {1, 4} в 5, 2 и 3, т.е. во все остальные вершины, в соответствии с определением). Трёхэлементными внешне ус-тойчивыми множествами являются только множества {1, 2, 4}, {1, 3, 4}, {1, 4, 5} (содержащие {1, 4}). Далее, внешне устойчивыми четырёхэлементными множествами являются {1, 2, 3, 4}, {1, 3, 4, 5} и {1, 2, 4, 5} и, наконец, {1, 2, 3, 4, 5}.

В данном графе есть единственное ядро: двухэлементное множества {1, 4}■

Само существование ядра для орграфов, в отличие от неориентированных графов, как ука-зывалось выше, не гарантировано, что демонстрирует следующий

Пример 9. Рассмотримпростойорграф без петель, показанный на рис.9. Проверим, что у

него нет ядра. Предположим, что ядро состоит из одной вершины 1. Но тогда нет дуги, ведущей из 1 в 3, т.е. оно не является внешне устойчивым. Аналогично, ядро не может состоять из вер-шины 2 или вершины 3. Предположим, что ядро состоит из двух вершин, скажем, вершин 1 и 2. Тогда есть дуга из 2 в 3, т.е. оно является внешне устойчивым. Но оно не является внутренне устойчивым, так как в него входят вершины 1 и 2, соединённые дугой. Аналогично для мно-жеств {1, 3} и {2, 3}. Наконец, множество всех вершин {1, 2, 3} является внешне устойчивым, но не является внутренне устойчивым. Таким образом, в данном орграфе ядер нет ■

Задание 3. Ворграфах, показанных на рис.10, найти

1) одно максимальное и одно минимальное по числу вершин ядро;

2) если все ядра содержат одно и то же число вершин, найти два разных ядра;

3) если имеется всего одно ядро, найти его;

4) если ядер не существует, объяснить этот факт ■

Дата добавления: 2015-10-16