Высказывательные формы

Высказывательные формы были определены в предыдущем разделе как формы, которые обозначают высказывания, т.е. являются высказываниями. Например, выражение

A 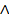(x > 3)

естественно считать двухместной высказывательной формой с высказывательной переменной A и числовой переменной x. Для случаев (которые нельзя априори исключать), когда на некото-рых наборах значений переменных высказывательная форма неопределенна, доопределим её логическим значением «Ложь» (т.е. значением F из двухэлементногомножества { T, F }). Поэто-му далее рассматриваются только всюду определённые высказывательные формы. Введённые в разделе 1-2.1 операции над высказываниями очевидным образом можно рассматривать и как операции над высказывательными фор­мами. 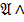Для любых высказывательных форм и и без специ­альных пояснений ясен смысл форм: Ø , , , → , , 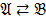Å .

Пусть (x ₁, …, x_s) – s -местная (s ≥l) высказыватель­ная форма, где x ₁, …, x_s – переменные формы , выписанные в каком-нибудь порядке. Пусть областью определения перемен­ной x_i бу-дет множество М_i (i = 1, …, s). Тогда областью ис­тинности высказывательной формы назы-

вается и как

или

(x 1, …, xs)

обозначается множество тех кортежей á a 1, a 2,..., as ñ, для ко-

торых (a ₁, …, a_s) истинно.

Понятие области истинности позволяет связать операции над множествами с операциями над высказывательными фор­мами. Так, очевидно, при s ≥ 1

(x 1, …, xs) (x 1, …, x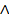s)

=

(x 1, …, xs)

(x 1, …, xs),

(x 1, …, xs) (x 1, …, xs)

=

(x 1, …, xs)

(x 1, …, xs).

Если М_i – обласги значений переменных x_i (i = 1, …, s), то

Ø (x 1, …, xs)

=

(x 1, …, xs)).

Задание 2. Для данных высказывательных форм найти области истинности.

1. (x, y): x ² + y ² ≥ 2 xy

2. (x, y): x + y ≥ 2 xy

3. (x, n): xⁿ > 1 + n (x – 1)

4. (x, y) → (x, y)

5. (x, n): x < n

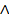
6. (x, n) (x, n) ■

Вернёмся к вопросу о способах задания множеств, упомянутому в разделе 2-1. Задание множества описанием характеристических свойств его элементов используется очень часто. В примерах 3-8, 3-9, 3-15 и 3-16 именно так задавались бесконечные графики. Теперь можно дать более детальное описание этого способа задания множеств. Именно, во многих случаях описываемое множество естественно совпадают с областью истинности некоторой высказыва-тельной формы. В примере 3-8 рассматривалось множество М точек á x, y ñ на плоскости, удов-летворяющих условию x ² + y ²= 1 (т.е. М – это окружность единичного радиуса с центром в начале координат). Определим высказывательную форму (x, y): x ² + y ² = 1. Понятно, что рас-сматриваемое множество М совпадает с областью истинности данной высказывательной фор-мы. В пункте 5) примера 1 высказывательная форма (x): x > 3 определяет бесконечное мно-жество чисел, бóльших 3.

Вообще, в тех случаях, когда интересующее нас множество М совпадает с областью ис-тинности некоторой высказывательной формы , это множество М именно так и может быть задано. Для этого используется стандартное обозначение

М = { x | (x)}, (1)

которое читается так: М – это множество элементов x, для которых высказывательная форма истинна. В формуле (1) x = á x ₁, x ₂,..., x_s ñ – это набор переменных данной высказывательной фор-мы. Более сложные вопросы проверки истинности произвольной высказывательной формы, приводящие, в частности, к формальному определению одного важного класса высказыватель-ных форм – предикатов – здесь не рассматриваются.

Задание 3. Нарисовать на координатной плоскости область истинности высказывательной формы (x, y) с числовыми переменными x, y, если

1. (x, y): y = x ².

2. (x, y): 2 x + 3 y – 1 > 0.

3. (x, y): sin(x + y) = 0.

4. (x, y): y = x ² + 1 ∕ x.

5. (x, y): y < x ² + 1 ∕ x.

6. (x, y): y = .

7. (x, y): y = ■

Дата добавления: 2015-10-16