Графики

Одним из важнейших понятий в дискретной – и не только дискретной – математике явля-ется понятие графика. График - это множество пар, т.е. множество, элементами которого служат пары. Вспоминая (см. раздел 1), что пара – это кортеж длины 2, можно сказать, что гра-фиком называется любое множество кортежей длины 2. Как и рассмотренное в разделе 3 поня-тие проектирования, понятия графика также является обобщением хорошо известного «школь-ного» понятия графика функции.

Пример 9. Вспомним хорошо известный график функции y = sin x. По построению, такой график состоит из всех пар чисел á x, y ñ (точек), таких, что y = sin x. Поэтому, как и любое мно-жество точек на плоскости, график данной функции является графиком и в смысле введённого определения, т.е. он является множеством пар ■

Заметим, что множества точек на плоскости из примеров 8 и 9 являются бесконечными. Они задаются не перечислением, а условиями на принадлежащие им элементы – набором характеристических свойств, т.е. таким набором свойств, которым обладают только элементы рассматриваемого множества. Подробнее такой способ задания множеств будет рассмотрен далее, в разделе 4-2.

Областью определенияграфика G называется множество ПР₁ G, а областью значений графика G - множество ПР₂ G. Таким образом, нахождение областей определения и значений графика сводится к операции проектирования кортежей длины 2 на одну из двух осей. Эта опе-рация является частным случаем операции проектирования (проектирование на одну ось), рас-смотренной в разделе 3.

Задание 3. Найти области определения и значения следующих графиков.

1. y = sin x.

2. {á p, q ñ, á q, q ñ, á q, a ñ, á p, a ñ}.

3. y = arcsin x.

4. {á a, c ñ, á b, p ñ, á q, f ñ, á{ a }, á q ññ}.

5. y = tg x.

6. {á b, x ñ, á a, n ñ, á x, b ñ, á d, a ñ}.

7. y = arcctg x.

8. {á x, x ñ, á l, a ñ, á x, b ñ}.

9. y = ln(1 - x ²).

10. {á b, c ñ, á b, b ñ, á d, c ñ}■

4.1. Операции над графиками. Рассмотрим две важные операции над графиками: одно-местную - инверсию, и двухместную - композицию. Инверсия графика определяется через ин-версию пары. Пара á с, d ñ называется инверсией пары á a, b ñ, eсли с = b, d = а. Другими словами, инверсией пары á a, b ñ является пара á b, a ñ. Инверсия пары a обозначается через a ^-1. Легко ви-деть, что (a ^-1)^-1 = a. Инверсией графика G называется множество инверсий всех пар из G. Инверсия графика G обозначается через G ^-1. График называется симметрическим, если G = G ^-1. Для симметрических графиков истинны следующие два высказывания: a Î G D a Î G ^-1 и a Î G D a ^-1Î G (напомним, что знаком D обозначена определённая в разделе 1-2.1.5 операция «эквивалентность» над истинностными значениями высказываний). Легко видеть также, что истинность любого из этих двух высказываний влечёт равенство G = G ^-1.

Задание 4. Найти инверсии следующих графиков.

1. {á a, b ñ, á n, c ñ, á b, q ñ}.

2. {á a, d ñ, á b, c ñ, á b, b ñ}.

3. {á b, b ñ, á l, n ñ, á n, b ñ}.

4. {á x, z ñ, á a, l ñ, á x, yñ, á z, x ñ}.

5. {á b, n ñ, á r, p ñ, á m, b ñ, á p, b ñ} ■

Пример 10. Пусть X – произвольное множество. Рассмотрим множество X^D всех пар вида á x, x ñ, где х Î X. Легко видеть, что X^D – симметрический график. Он называется диагональю множества X ².

Введём необходимые понятия. Пусть α = á p, q ñ, β = á s, t ñ – две пары. Композицией α○β пар α и β (в указанном порядке) называется пара γ, определяемая следующим образом:

γ = , (1)

где Λ – пустой кортеж (см. раздел 1.1).

Пример 11. Композицией пар α = á p, q ñ и β = á q, r ñ при любых p, q и r в соответствие с формулой (1) является пара γ = á p, r ñ. Композицией пар β = á q, r ñ и α = á p, q ñ при p = r является пара á q, q ñ. Композицией пар β = á q, r ñ и α = á p, q ñ при p ≠ r является пустой кортеж Λ. Компози-цией пар α = áá p, r ñ, q ñ и β = á q, r ñ является пара áá p, r ñ, r ñ. Действительно, формула (1) при q = s определяет пару á p, t ñ при произвольных p и t. В данном случае на первом месте (вместо p) сто-ит пара á p, r ñ, а на втором месте (вместо t) стоит элемент r. Ещё раз почеркнём, что компонен-тами кортежа могут быть любые объекты, включая множества и другие кортежи ■

Задание 5. Найти композицию пар в указанном и обратном порядке:

1. á n, c ñ○á c, c ñ.

2. á a, d ñ○á b, b ñ.

3. á a, b ñ○á b, a ñ.

4. á b, a ñ○á a, b ñ.

5. á l, n ñ○á n, b ñ.

6. á n, b ñ○á l, n ñ.

7. á b, x ñ○á x, f ñ.

8. á b, x ñ○á x, á f ññ.

9. á{ b }, x ñ○á x, f ñ.

10. á b, x ñ○á y, f ñ ■

Исходя из операции композиции двух пар, введём теперь операцию композицию двух графиков, т.е. множеств пар (см. определение графика). Композиция R = P ○ Q определяется как множество композиций всех пар из P со всеми парами из Q. Формально:

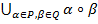P Q = , (2)

где композиция двух пар α○β определена формулой (1).

Пример 12. Пусть график P = {á a, b ñ, á a, c ñ}, график Q = {á b, b ñ, á d, c ñ}. Найдёмкомпози-цию графиков P ○ Q. Имеем в соответствии с формулой (2) P ○ Q = {á a, b ñ○á b, b ñ, á a, b ñ○á d, c ñ, á a, c ñ ○á b, b ñ, á a, c ñ○á d, c ñ}. В соответствии с формулой (1) для композиций двух пар имеем

á a, b ñ○á b, b ñ = á a, b ñ, á a, b ñ○á d, c ñ = á a, c ñ○{á b, b ñ = á a, c ñ○á d, c ñ = Λ.

Поэтому P ○ Q = {á a, b ñ} (множество пар из P ○ Q состоит из одной пары á a, b ñ).

Найдём теперь композицию графиков Q ○ P при тех же самых Q и P. Имеем Q ○ P = {á b, b ñ○ á a, b ñ, á b, b ñ○á a, c ñ, á d, c ñ○á a, b ñ, á d, c ñ○á a, c ñ} = Λ. В этом порядке композиция оказалась пустой ■

Задание 6. Найти композицию графиков в указанном и обратном порядке:

1. P = {á a, b ñ, á n, c ñ}, Q = {á b, n ñ, á c, c ñ}.
2. P = {á a, d ñ, á b, c ñ}, Q = {á b, b ñ, á d, c ñ}.
3. P = {á a, x ñ, á x, x ñ}, Q = {á x, b ñ, á b, a ñ}.
4. P = {á y, d ñ, á y, c ñ}, Q = {á c, b ñ, á z, y ñ}.
5. P = {á a, b ñ, á a, c ñ}, Q = {á b, b ñ, á d, c ñ}.
6. P = {á b, n ñ, á l, n ñ}, Q = {á n, b ñ, á d, c ñ}.
7. P = {á n, b ñ, á c, n ñ}, Q = {á n, b ñ, á b, c ñ}.
8. P = {á a, b ñ, á a, c ñ}, Q = {á b, b ñ, á d, a ñ}.
9. P = {á a, b ñ, á n, c ñ}, Q = {á b, n ñ, á c, c ñ}.
10. P = {á b, b ñ, á l, n ñ}, Q = {á n, b ñ, á d, l ñ}.
11. P = {á a, a ñ, á a, c ñ}, Q = {á b, a ñ, á c, a ñ}.
12. P = {á b, x ñ, á a, n ñ}, Q = {á x, b ñ, á d, a ñ}.
13. P = {á x, x ñ, á l, a ñ}, Q = {á x, f ñ, á y, x ñ}.
14. P = {á b, b ñ, á a, l ñ}, Q = {á x, b ñ, á l, a ñ}.
15. P = {á r, n ñ, á r, r ñ}, Q = {á m, b ñ, á d, r ñ}.
16. P = {á b, x ñ, á a, n ñ}, Q = {á b, b ñ, á p, q ñ}.
17. P = {á x, x ñ, á a, l ñ}, Q = {á x, yñ, á y, x ñ}.
18. P = {á b, b ñ, á a, n ñ}, Q = {á x, y ñ, á b, a ñ}.
19. P = {á b, n ñ, á l, n ñ}, Q = {á x, b ñ, á n, a ñ}.
20. P = {á b, x ñ, á a, n ñ}, Q = {á n, b ñ, á d, c ñ}.
21. P = {á x, x ñ, á l, a ñ}, Q ={á x, b ñ, á l, b ñ}.
22. P = {á f, b ñ, á a, l ñ}, Q = {á x, f ñ, á y, x ñ}.
23. P = {á b, n ñ, á r, p ñ}, Q = {á m, b ñ, á p, b ñ}.
24. P = {á b, x ñ, á q, n ñ}, Q = {á d, r ñ, á p, q ñ}.
25. P = {á x, z ñ, á a, l ñ}, Q = {á x, yñ, á z, x ñ}.
26. P = {á b, b ñ, á a, n ñ}, Q = {á x, b ñ, á a, a ñ} ■

Для бесконечных графиков формула (2) остаётся в силе, однако непосредственное рас-смотрение всех пар из P и Q (как это делается в примере 12) невозможно. Однако для нахожде-ния композиции P ○ Q можно воспользоваться следующим простым соображением, справедли-вым для произвольных графиков.

Утверждение 1. Пара á x, y ñÎ P ○ Q тогда и только тогда, когда существует элемент z, такой, что á x, z ñÎ P и á z, y ñÎ Q ■

Пример 13. Рассмотрим композицию двух графиков P и Q: y = sin x и y = ln x. В соответст-вии с вышесказанным, пара чисел á x, y ñÎ P ○ Q тогда и только тогда, когда существует элемент z, такой, что z = sin x и y = ln z. В данном случае это означает, что ln(sin x) определён, что может быть при любом x, для которого sin x > 0. А для последнего необходимо и достаточно, чтобы вы-полнялось условие 2 kπ < x < (2 k +1) π для какого-нибудь целого числа k. Соответствующее значение y из пары á x, y ñÎ P ○ Q определяется формулой y = ln(sin x) ■

Пример 13 показывает, что достаточно сложное – на первый взгляд – понятие композиции двух графиков является обобщением хорошо известного «школьного» понятия суперпозиции двух функций.

Если у нас имеется три графика: P, Q и R, то с помощью операции композиции двух гра-фиков из них можно определить два разных графика: (P ○ Q)○ R и (P ○(Q ○ R). Имеет место

Утверждение 2. Графики (P ○ Q)○ R и P ○(Q ○ R) совпадают, т.е. состоят из одних и тех же пар ■

Утверждение 2 выражает важное свойство операции композиции – её ассоциативность. Это означает, что в выражениях (P ○ Q)○ R и P ○(Q ○ R), как и в более сложных выражениях такого же типа, можно убрать скобки и рассматривать композицию не только двух, но и любого числа графиков: P ○ Q ○ R, P ○ Q ○ R ○ S, и т.д.

4.2. Свойства графиков. График называется функциональным (инъективным), если в нем нет пар с одинаковыми первыми (соответственно одинаковыми вторыми) компонентами.

Пример 14. График {á b, b ñ, á a, n ñ} является функциональным, поскольку в обеих входя-щих в него парах и первые, и вторые компоненты являются разными: b ≠ a (первые компонен-ты) и b ≠ n (вторые компоненты). Заметим, что совпадение компонент в паре á b, b ñ никак не влияет на рассматриваемые свойства. График {á x, b ñ, á x, a ñ} не является функциональным, но является инъективным (первые компоненты совпадают, а вторые – нет). График {á n, с ñ, á d, c ñ} является функциональным, но не является инъективным (вторые компоненты совпадают, а пер-вые – нет). Наконец, график {á n, b ñ, á n, с ñ, á d, c ñ}, состоящий из трёх пар, не является ни функци-ональным (поскольку он содержит пары á n, b ñ и á n, с ñ с совпадающими первыми компонента-ми), ни инъективным (поскольку он содержит пары á n, с ñ и á d, c ñ с совпадающими вторыми ком-понентами) ■

Пример 15. Рассмотрим график, состоящий из всех точек á x, y ñ, удовлетворяющих уравне-нию окружности x ² + y ² = 1. Этот график не является ни функциональным (поскольку он содер-жит пары á0, 1ñ и á0, –1ñ с совпадающими первыми компонентами), ни инъективным (поскольку он содержит пары á1, 0ñ и á–1, 0ñ с совпадающими вторыми компонентами) ■

Пример 16. Рассмотрим график, состоящий из всех точек á x, y ñ, удовлетворяющих уравне-нию y = ln(x). Этот график является функциональным и инъективным, поскольку он является графиком строго возрастающей функции (т.е. (x ₁ ≠ x ₂) D (y ₁ ≠ y ₂)) ■

Задание 7. Для всех графиков из заданий 3, 4 и 6 проверить наличие (или отсутствие) свойств функциональности и инъективности (см. примеры 14 – 16) ■

Задание 8. Для всех графиков из задания 6 найти проекции ПР₁ G, ПР₂ G ■

---

Дата добавления: 2015-10-16