Множества и подмножества

Понятие множества (как и уже рассмотренное понятие высказывания) является для нас ис-ходным, неопределяемым. Можно говорить о множестве студентов в данной аудитории, мно-жестве книг в библиотеке и т.д. Множество составлено из элементов, способных обладать неко-торыми свойствами и находиться между собой и с элементами других множеств в неких отно-шениях. Важно, что элементы множества являются различными и (хотя бы в принципе) разли-чимыми. Мы будем обозначать сами множества прописными, а их элементы – строчными бук-вами латинского алфавита. Высказывание «х есть элемент множества X» символически записы-вают так: х Î X. Эта связь между элементом и множеством называется принадлежностью. От-рицание этого высказывания записывают так: х Ï X. Множества X и Y называют равными, если они состоят из одних и тех же элементов. Высказывание о равенстве множеств X и Y записыва-ют в виде: X = Y, а отрицание этого высказывания (т.е. высказывание, состоящее в том, что мно-жества X и Y не равны) – в виде X ≠ Y.

Для удобства вводят так называемое пустое множество, т.е. множество, не содержащее элементов. Его изображают символом Æ. Таким образом, если х – некоторый объект, то принад-лежность х ÎÆ – всегда ложное высказывание. Наряду с пустым множеством полезно ввести в рассмотрение и так называемое универсальное множество. Это множество состоит из всех элементов, имеющих отношение к определённой рассматриваемой ситуации. Например, при анализе успеваемости (или проведении социологического опроса) студентов в качестве универ-сального выступает множество всех студентов данного института или города; в экономическом исследовании в качестве универсального часто выступает множество всех фирм данной страны или группы стран, и т.д. Универсальное множество обычно обозначается буквой U. Заметим, что при переходе от одной ситуации к другой универсальное множество (в отличие от пустого множества) может измениться.

Может случиться так, что все элементы множества X являются одновременно элементами множества Y, т,е.

х Î X ® х Î Y. (1)

В этом случае говорят, что X есть подмножество, или часть Y, что записывается так:

X Í Y. (2)

Из (1) и (2) получаем, что X Í Y тогда и только тогда, когда истинна импликация х Î X ® х Î Y. Из определения операции эквивалентности следует, что (X = Y) 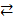(X Í Y)Ù(Y Í X). Отрица-ние высказывания (2) записывается как X Ë Y. X Ì Y означает, что (X Í Y)Ù(X ≠ Y).

Множество может быть задано перечислением своих элементов, порождающей процеду-рой или описанием свойств, которыми должны обладать его элементы (разрешающей процеду-рой). В настоящей главе будут рассматриваться только конечные множества. Конечное множес-тво можно задать (хотя бы в принципе) списком, в котором и перечисляются все его элементы. Список заключается в фигурные скобки, а сами элементы отделяются друг от друга запятыми. Другие способы задания множеств будут рассмотрены далее (в частности, в разделе 4-2).

Пример 1. Множество имён летних месяцев: {июнь, июль, август} ■

Пример 2. В описаниях «больших» конечных множеств используются многоточия. Мно-жество неотрицательных целых чисел, не превосходящих 50, записывают как {0, 1, …, 50}. За-метим, что почёркнутые в предыдущей фразе слова как раз описывают свойство всех элементов данного множества, выделяющее их из всех остальных объектов. Такие свойства называются «характеристическими» ■

Пример 3. Многоточия можно использовать только в тех случаях, когда не возникает дву-смысленности. Если A = {3, 5, 7, …, 19}, то не ясно, является ли A множеством нечётных чисел, лежащих в интервале от 3 до 19, или это множество простых чисел из того же интервала, т.е. возможны разные «расшифровки» неопределённости, скрывающейся за многоточием ■

Обратим внимание на следующее. Элемент a надо отличать от одноэлементного множест-ва { a }: это объекты разной природы. Нельзя написать, что a ={ a } или a Í{ a }. Но можно на-писать истинное высказывание a Î{ a }. Элементами множеств могут быть другие множества. Множество, элементами которого служат все подмножества множества X, обозначается симво-лом B (Х). Его называют булеаном множесгва X.

Задание 1. Определить истинность или ложность следующих высказываний:

1. 6 Î{–2, 5, 8, 9}

2. 9 Ï{6, 3, 4, 8}

3. { k, c, r, a } = { k, c, a, r }

4. Множество натуральных чисел, меньших трёх ¹ {1, 2}

5. 8 Í {3, –2, 5, 7, 8}

6. {5, 8, 9}Î{5, 8, 9, 0}

7. 6 ¹ {–2, 5, 8, 9}

8. Æ = {Æ}

Пусть A = {2, 4, 6, 8, 10, 12}, B = {2, 4, 8, 10, 12}, C = {4, 10, 12}.

9. 4Î A

10. 8Î B

11. 4Ï C

12. Каждый элемент C принадлежит A

13. Каждый элемент C принадлежит B

Пусть U = { a, b, c, d, e, f, g }, A = { a, e }, B = { a, b, e, f, g }, C = { b, f, g }, D = { d, e }.

14. C Ì U

15. D Í B

16. A Ì B

17. B Í C

18. ÆÌ A

19. ÆÍÆ

20. D Ì B

21. D Ë B

22. A Ë B ■

Пример 4. Вставить знак , , Î или Ï вместо пробела, чтобы получить истинное выс-казывание:

(a) {3, 4, 5, 6} _______ {3, 4, 5, 6, 8}.

Поскольку каждый элемент множества {3, 4, 5, 6} принадлежит и множеству {3, 4, 5, 6, 8}, то 1-ое множество является подмножеством 2-го, так что надо вставить Í.

(b) 1 _______ {2, 4, 6, 8}.

Элемент 1 не принадлежит множеству {2, 4, 6, 8}. Поэтому между ними надо вставить Ï ■

Задание 2. Вставить знак Î, Ï, = или ¹ вместо пробела, чтобы получить истинное выска-зывание:

1. 5____{2, 4, {5}, 7}

2. {4}____{4, 7, 8, 12}

3. 0____{1, –2, 0, {5}, 9}

4. {3}____{2, 3, 4, 6}

5. 8____{3, –2, 5, 7, 8}

6. –12____{3, 8, 12, 18}

7. 3____{2, 5, 6, 8}

8. b ____{ h, c, d, a, b }

9. 9____{6, 3, 4, 8}

10. { k, c, r, a }____{ k, c, a, r }

11. {5, 8, 9}____{5, 8, 9, 0}

12. 6____{–2, 5, 8, 9}

13. m ____{ l, m, n, o, p }

14. { e, h, a, n }____{ a, { h }, e, n }

15. {3, 7, 12, 14}____{3, 7, 12, 14, 0}■

Задание 3. Вставить знак Í или Ë вместо пробела, чтобы получить истинное высказыва-ние:

1. {4}____{4, 7, 8, 12}

2. {3}____{2, 3, 4, 6}

3. { k, c, r, a }____{ k, c, a, r }

4. {5, 8, 9}____{5, 8, 9, 0}

5. { e, h, a, n }____{ a, { h }, e, n }

6. {3, 7, 12, 14}____{3, 7, 12, 14, 0}

7. {–2, 0, 2}_____{–2, –1, l, 2}

8. {Понедельник, Среда, Пятница}_____{Воскресенье, Понедельник, Вторник, Среда, Четверг}

9. { a, n, d }_____{ r, a, n, d, y }

10. Æ_____{ a, b, c, d, e }

11. Æ_____Æ

12. {–7, 4, 9}_____множество всех нечётных целых чисел

13. { B, C, D }_____{ B, C, D, F }

14. {красный, зелёный, синий, жёлтый}_____{ зелёный, жёлтый, синий, красный}

15. Æ_____{0}

16. {–1, 0, 1, 2, 3) _____{0, 1, 2, 3, 4} ■

Задание 4. Написать булеан(множество всех подмножеств) для следующих множеств:

1. { B, C, D }

2. { B, C }

3. { B, { C }}

4. {{ B },{ C }}

5. { B, { B }}

6. { B, { B }, C }

7. {{Æ}, B, { C }}

8. { a, 1, 0}

9. { a, 1, {0}}

10. { a, { a }, 1, {0}}

11. {–3, 3, {–3}}

12. {Понедельник, Среда, Пятница}

13. {Понедельник, Среда, August}

14. { e, é, è } ■

Дата добавления: 2015-10-16