Алгебраические свойства операций над множествами

Введенные выше операции над множествами обладают рядом свойств. Приведем основные из них:

– коммутативность;

1) А È В = В È А

А Ç В = В Ç А

– ассоциативность;

2) А È (В È С) = (А È В)È С

А Ç (В Ç С) = (А Ç В)Ç С

– дистрибутивность;

3) А È (В Ç С) = (А È В)Ç (А È С)

А Ç (В È С) = (А Ç В)È (А Ç С)

4) А È Æ = А;

5) А È V = V;

6) А Ç Æ = Æ;

7) А Ç V = А;

8) А È = V;

9) А Ç = Æ;

10) Æ = V;

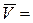11) Æ.

Доказательство этих свойств (формул) состоит в том, что берут произвольный элемент множества левой части и доказывают, что он принадлежит и множеству правой части, и наоборот.

Операции над множествами обладают принципом двойственности, т.е. если справедливо некоторое соотношение между множествами, то справедливо и «двойственное» соотношение, полученное из данного путем взаимной замены всюду знаков Ç и È, V и Æ, Ì и É.

Примерами двойственных соотношений являются соотношения в группах 1), 2), 3), соотношения 4) и 7), 5) и 6), 8) и 9), 10) и 11).

Лекция 2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

План:

1. Высказывания. Логические операции над высказываниями.

2. Формулы логики высказываний.

3. Основные эквивалентные преобразования формул (законы логики высказываний).

Дата добавления: 2015-10-21