УПРАЖНЕНИЯ. Найти: а) А È В È С; б) А Ç В Ç С; в) А \ (В È С); г) (А \ В) È С; д) (А È В) \ (А

1. Пусть А = {1, 2}, В = {2, 3}, С = {1, 3}.

Найти: а) А È В È С; б) А Ç В Ç С; в) А \ (В È С); г) (А \ В) È С;
д) (А È В) \ (А Ç В).

2. Пусть V = { а, b, c, d, е }, А = { а, c }, В = { а, b, d }, С = { b, c, е }.

Найти: а) А Ç ; б) (А Ç С) È ; в) А È С; г) Ç ; д) ;
е) А \ ; ж) (А \ С) È (В \ С).

3. Доказать справедливость следующих равенств:

а) А È (А Ç В) = А, А Ç (А È В) = А – законы поглощения;

б) = Ç , = È – законы Де Моргана.

4. В юридической фирме работают 3 адвоката. Проверка документации показала, что над каждым делом в октябре работало ровно 2 адвоката. Известно, что 1-й работал над 70 делами, 2-й – над 85, а 3-й – над 45 делами. Сколько дел вела фирма в октябре?

5. В группе 22 человека посещают кружок по гражданскому праву, 20 чел. – по трудовому праву и 5 человек посещают оба кружка. При этом 10 человек вообще не посещают кружки. Сколько человек в группе?

6. В группе каждый студент изучает 2 языка (английский, испанский, китайский). 12 ходят одновременно на испанский и английский языки. При этом 26 человек изучают английский, а 30 – испанский языки. Сколько человек в группе? Сколько человек изучают одновременно английский и китайский? Сколько человек изучают китайский язык?

7. Записать формулой следующее сложное высказывание: «Этот человек финансист или юрист».

8. Написать таблицы истинности для следующих формул логики высказываний:

а) F = (Х «У) ® Х Ù У;

б) F = (Х Ù У) Ú ® (Х Ú Z);

в) F = (У ® Z) «(Х Ú У) Ù .

9. Доказать равносильность формул:

а) Х Ù У = ;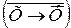

б) Х Ú У = .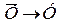

10. Упростить формулу (Х Ù У) Ú (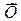 Ù У) Ú (Х Ù ).

ЛИТЕРАТУРА

Москинова Г. И. Дискретная математика.– М.: Логос, 2007.

Тихомиров Н. Б., Шелехов А. М. Математика: учебный курс для юристов.– М.: Юрайт, 2000.

Метельский Н. В. Дидактика математики.– Мн.: БГУ, 1982.

СОДЕРЖАНИЕ

Лекция 1. Множества и операции над ними.................................... 3

1. Основные понятия......................................................................... 3

2. Операции над множествами.......................................................... 5

3. Алгебраические свойства операций над множествами................ 6

Лекция 2. Элементы математической логики................................. 7

1. Высказывания. Логические операции над высказываниями....... 7

2. Формулы логики высказываний................................................... 9

3. Основные эквивалентные преобразования формул (законы логики высказываний)............................................................................................ 12

Упражнения...................................................................................... 15

Литература...................................................................................... 15

— –

Учебное издание

Дата добавления: 2015-10-21