Ключевые понятия

Множество. Способы задания множеств. Операции объединения, пересечения, дополнения. Разность множеств.

Основные понятия

Понятие множества относится к числу первичных математических понятий, т.е. это понятие не имеет логического определения через более простые понятия.

Под множеством понимают совокупность некоторых объектов, объединенных по определенному признаку. Так, можно говорить о множестве студентов института, о множестве книг в библиотеке, о множестве всех натуральных чисел.

Объекты, из которых состоит множество, называются его элементами.

Множество обозначают прописными буквами, а их элементы – строчными буквами.

Принадлежность элемента а множеству М обозначается а Î М, непринадлежность а Ï М или а 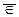М.

Множество А называется подмножеством множества В, если каждый элемент из А является элементом В (рис. 1). Обозначается А Ì В.

Запись А Ì В означает, что А является подмножеством множества В, не совпадающим с В.
В этом случае множество А называется собственным подмножеством множества В.

Множества А и В равны (А = В), если А Ì В
и В Ì А.

Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным (например, множества натуральных, целых, вещественных чисел – бесконечные множества).

Мощность множества – число элементов в конечном множестве. Обозначение ç А ÷.

Понятие мощности множества вводится также и для бесконечных множеств. Однако здесь это обобщение мы рассматривать не будем.

Множество, не содержащие ни одного элемента, называется пустым множеством, обозначается символом Æ. Полагают, что мощность пустого множества равна нулю, т. е. çÆ÷ = 0. Кроме того, полагают, что пустое множество является собственным подмножеством любого множества.

Примером пустого множества является множество действительных решений уравнения х ² + 1 = 0.

Множество определяется либо путем записи его элементов в фигурных скобках (т. е. в фигурных скобках перечислены все элементы множества), либо указанием общего свойства, которым обладают все элементы данного множества.

Например, запись А = { а, b, c, d } означает, что множество А состоит из четырех элементов а, b, c и d; запись А = {1, 2, 4, 8, 16, …} означает, что множество А состоит из всех целых чисел, являющихся целыми степенями двойки; запись А = {2, 4, 6, …, 100} означает, что множество А состоит из четных чисел, не превышающих 100; запись А = { х: х Î R и 0 £ х £ 4} означает, что множество А состоит из всех действительных чисел, удовлетворяющих неравенству 0 £ х £ 4.

Определение множества В = {1, 2, 3, 3, 7} является некорректным, так как при перечислении элементов не следует указывать один и тот же элемент несколько раз.

Пример. Принадлежит ли элемент а множеству В, если известно, что
А = { а, b, c, d }, В = { А, С }?

Решение. а Ï В, так как элемент а не перечислен в списке элементов множества В.

С понятием «множество» следует обращаться достаточно осторожно, так как свободное обращение с ним может привести к противоречиям (парадоксам). Например, предположение о существовании множества всех множеств приводит к противоречиям.

Другой пример (парадокс брадобрея): в некотором городе брадобрей бреет всех, кто сам не бреется, и не бреет тех, кто сам бреется. К какому множеству отнести брадобрея: кто бреется сам либо бреется у брадобрея?

Для избежания подобных противоречий будем предполагать существование в каждом конкретном случае так называемого универсального множества (универсума) V, такого, что рассматриваемые системы множеств являются его подмножествами.

Например, для множеств целых Z, рациональных Q, натуральных чисел N в качестве универсума можно принять множество действительных чисел R:

N Ì Z Ì Q Ì R.

Дата добавления: 2015-10-21