Читайте также:
|
В предыдущем разделе было продемонстрировано, как по составному высказыванию по-строить его формальное представление – сопровождающую формулу. Напомним, что в такую формулу входят символы простых высказываний, из которых построено данное составное вы-сказывание. Эти символы соединены знаками операций (все шесть операций рассмотрены в разделе 2.1). Используя таблицы 2 – 7, при любых значениях истинности простых высказыва-ний можно определить истинность рассматриваемого составного высказывания. Подчеркнём, что в отличие от процедуры построения самой сопровождающей формулы, вычисление истин-ностных значений данного высказывания по уже построенной сопровождающей формуле явля-ется совершенно чёткой и однозначной процедурой.
В основе рассматриваемой здесь конструкции лежит построение так называемых таблиц истинности составных высказываний по сопровождающим их формулам, аналогичным фор-мулам (1) – (5). Таблицы истинности для 6-и базовых операций уже были определены в разде-лах 2.1.2 – 2.1.7. Таблицы истинности для произвольных составных высказываний оказываются во многом похожи на эти таблицы. Цель у общих таблиц такая же, как у 6-и базовых: выразить истинность составного высказывания через значения истинности входящих в них простых вы-сказываний.
Начнём с составных высказываний, сопровождающие функции которых содержат только два разных буквенных символа. Таблицы истинности для таких высказываний содержат 4 «ра-бочие» строки, как и таблицы 3 – 7 из раздела 2.1. Левая часть любой такой таблицы истин-ности (размерности 2) будет такова:
Таблица 9
| p | q |
| T | T |
| T | F |
| F | T |
| F | F |
Заметим, что здесь (как и в таблицах 3 – 7) строчные буквы p и q обозначают не сами произ-вольные простые высказывания, а их истинностные (или логические) значения. Этим простым высказываниям сопоставлены два столбца таблицы 9. Строчки таблицы соответствуют всем возможным сочетаниям значений для двух высказываний. Таким образом, в 1-ой строке оба высказывания истинны; во 2-ой строке первое высказывание истинно, а второе – ложно; в 3-ей строки первое высказывание ложно, а второе – истинно; в 4-ой строке оба высказывания ложны. Нетрудно понять, что этими четырьмя случаями действительно исчерпываются все комбинации истинностных значений двух высказываний.
Пример 16. Построим таблицу истинности для составного высказывания (P ® Q)Ù P (ещё раз напомним, что высказывание (P ® Q)Ù P – сокращённое обозначение для высказывания, сопровождающая функция которого имеет вид (P ® Q)Ù P).
Построим таблицу, начиная со стандартной левой части и затем последовательно заполняя столбцы слева направо, начиная с 1-го столбца (см. таблицу 10). При этом символы P и Q, обозначавшие простые высказывания, заменяются на строчные буквы p и q, равные истинност-ным значениям высказываний P и Q. Таким образом, в столбце 1) записываются значения им-пликации, т.е. в него просто подставляются значения из правого столбца таблицы 5. Далее, в соответствии с выражением (p ® q)Ù p, элементы столбца 1) умножаются на элементы столбца p этой же таблицы 10. В 1-ой строчке получается T Ù T = T, а в остальных строчках получаем F Ù T = T Ù F = T Ù F = F.
Таблица 10
| p | q | 1) p ® q | 2) 1Ù p |
| T | T | T | T |
| T | F | F | F |
| F | T | T | F |
| F | F | T | F |
■
Пример 17. Построим таблицу истинности для составного высказывания Ø P ÚØ Q. Вычис-ления продемонстрированы в таблице 11.
Таблица 11
| p | q | 1) Ø p | 2) Ø q | 3) 1Ú2 |
| T | T | F | F | F |
| T | F | F | T | T |
| F | T | T | F | T |
| F | F | T | T | T |
■
В случае, когда в составное высказывание входит не два, а три символа переменных, конс-трукция практически не изменяется. Разница лишь в том, что в левой стандартной части табли-цы истинности уже не четыре строчки, а восемь строчек. Дело в том, что число разных комби-наций истинностных значений трёх высказываний равно 23 = 8. Заметим, что для n высказыва-ний это число равно 2 n, однако будут рассмотрены только случаи n = 2, 3. Стандартная часть любой таблицы истинности с тремя простыми высказываниями представлена таблицей 12:
Таблица 12
| p | q | r |
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Пример 18. Построим таблицу истинности для составного высказывания (((P Ù Q)® R)Ù Ø R) ®(Ø P ÚØ Q), подробно рассмотренного в примере 4. Вычисления продемонстрированы в таблице 13.
Таблица 13. Построение таблицы истинности для высказывания (((P Ù Q)® R) ÙØ R) ®(Ø P ÚØ Q)
| p | q | r | 1) p Ù q | 2) 1® r | 3) Ø r | 4) 2Ù3 | 5) Ø p | 6) Ø q | 7) 5Ú6 | 8) 4®7 |
| T | T | T | T | T | F | F | F | F | F | T |
| T | T | F | T | F | T | F | F | F | F | T |
| T | F | T | F | T | F | F | F | T | T | T |
| T | F | F | F | T | T | T | F | T | T | T |
| F | T | T | F | T | F | F | T | F | T | T |
| F | T | F | F | T | T | T | T | F | T | T |
| F | F | T | F | T | F | F | T | T | T | T |
| F | F | F | F | T | T | T | T | T | T | T |
■
Пример 19. Построим таблицу истинности составного высказывания ((P → R)Ù(R → Q))→ (P → Q), называемого правилом силлогизма. Последовательные шаги показаны в таблице 14.
Таблица 14. Построение таблицы истинности для высказывания ((P → R)Ù(R → Q))→(P → Q)
| p | q | r | 1) p ® r | 2) r ® q | 3) 1Ù2 | 4) p ® q | 5) 3®4 |
| T | T | T | T | T | T | T | T |
| T | T | F | F | T | F | T | T |
| T | F | T | T | F | F | F | T |
| T | F | F | F | T | F | F | T |
| F | T | T | T | T | T | T | T |
| F | T | F | T | T | T | T | T |
| F | F | T | T | F | F | T | T |
| F | F | F | T | T | T | T | T |
■
Задание 4. Построить таблицы истинности для высказываний (1) – (5) (для некоторых из них они уже были построены в примерах из данного раздела) ■
Задание 5. Построить таблицы истинности для следующих составных высказываний:
1. Ø P Ù(Q ®Ø R)
2. (Ø R ÙØ Q)®(Ø P Ù Q)
3. (P ® R ÚØ Q
4. (Q ÚØ R)® P
5. (Ø P ® Q) ÚØ R
6. Ø(P Ù Q) Ù(R ®Ø Q)
7. Ø((Ø P ® Q)Ú R)
8. Ø(R Ú(Ø P ®Ø Q))
9. (Ø P ®Ø Q)Ú(Ø R ÙØ P)
10.Ø P ®(Q ÚØ R)
11. (Ø R ®Ø Q)Ú(Ø P Ù Q)
12. (P Ù R)®Ø Q
13. (Q ® R)Ù P
14. (Ø P Ù Q)®Ø R
15. Ø(P ® Q)Ù(R ÚØ Q)
16. Ø((Ø P Ù Q)® R)
17. Ø(R ®(Ø P ÙØ Q))
18. (Ø P ÙØ Q)Ú(Ø R ®Ø P)
19. (P ÙØ P) ® Q
20. ((P ® Q)Ù P)® Q
21. (P Ù Q)® R
22. ((P Ù Q)® R) ÙØ R
23. (P ® Q)® R
24. P ®(Q ® R)
25. (P ®Ø Q)® R
26. P ®(Ø Q ® R)
27. (P ®Ø Q)® Ø R ■
3.1. Равносильность составных высказываний. Пусть Α = Α(P, Q,..., Z) и Β = Β(P, Q,..., Z) - составные высказывания, построенные из высказываний P, Q,..., Z. Высказывания Α и Β называются равносилъными, что обозначается Α º Β, если их истинностные значения совпада-ют при любых комбинациях истинностных значений входящих в них высказываний P, Q,..., Z. Равносильность высказываний легко устанавливается при помощи таблиц истинности: если вы-сказывания Α и Β равносильны, то столбец значений истинности высказывания Α совпадёт со столбцом значений истинности высказывания Β (столбец значений истинности высказывания - это самый правый столбец таблицы истинности, соответствующей данному высказыванию).
Пример 20. Установим равносильность следующих двух составных высказываний:
Α = Ø P ÙØ Q и Β = Ø(P Ú Q)
Таблицы истинности для высказываний Α и Β представлены таблицами 15 и 16:
Таблица 15. Таблица истинности для высказывания Α
| p | q | 1) Ø p | 2) Ø q | 3) 1Ù2 |
| T | T | F | F | F |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
Таблица 16. Таблица истинности для высказывания Β
| p | q | 1) p Ú q | 2) Ø1 |
| T | T | T | F |
| T | F | T | F |
| F | T | T | F |
| F | F | F | T |
Совпадающие правые столбцы таблиц доказывают равносильность
Ø P ÙØ Q º Ø(P Ú Q). (6)
Верна и аналогично доказываемая равносильность (4):
Ø P ÚØ Q º Ø(P Ù Q). (7)
Равносильности (3) и (4) называются законами де Моргана, названными по имени английского логика Огюста де Моргана (1806 - 1871). Похожие выражения существуют в теории множеств и во многих разделах дискретной математики ■
Задание 6. Построив таблицы истинности, проверить равносильность следующих пар со-ставных высказываний:
1. P ÚØ P º T
2. Ø(Ø P) º P
3. P Ù F º F
4. P Ù P º P
5. P ÙØ P º F
6. P Ù T º P
7. P Ú F º P
8. P Ú P º P
9. P ÚØ P º T
10. P Ú T º T
11. P Ù Q º Q Ù P
12. P Ú Q º Q Ú P
13. P Ù(Q Ú R) º (P Ù Q)Ú(P Ù R)
14. P Ú(Q Ù R) º (P Ú Q)Ù(P Ú R)
15. Ø(P Ù Q) º Ø P ÚØ Q
16. Ø(P Ú Q) º Ø P ÙØ Q
17. Ø(P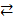 
Q) º P Å Q
18. Ø(P→Q) º P ÙØ Q
19. P→ Ø P º Ø P
20. P Ú(Ø P Ù Q) º P Ú Q
21. P ®(Q ® R) º (P Ù Q)® R
22. P ®(Q ® R) º (P Ù R)® Q
23. P ®(P Ú Q) º Q ®(P Ú Q) ■
В дальнейшем эти же равносильности будут использоваться при анализе других объектов, в том числе булевых, или логических функций. Обратим внимание, что в последней фразе сло-во «или» используется не в качестве логического союза. Живой язык всегда шире любого мате-матического!
Обратим особое внимание на разницу между понятиями эквивалентности и равносильнос-ти. Эквивалентность – это операция над двумя высказываниями; её результатом является новое высказывание, истинностное значение которого определяется таблицей 6. Равносильность – это логическое значение (истина или ложь), сопоставляемое двум составным высказываниям, зави-сящим от одних и тех же простых высказываний. Никакая комбинация этих двух высказыва-ний, в отличие от эквивалентности, при этом не определяется.
Составное высказывание называется тождественно истинным (тождественно лож-ным), если его истинностное значение истина (ложь) при всех комбинациях истинностных зна-чений исходных простых высказываний. Приведённое в примере 19 правило силлогизма - тождественно истинное высказывание. Тождественно истинные высказывание называются так-же тавтологиями. Высказывания с таблицами истинности 13 и 14 являются тавтологиями.
Если высказывание принимает как значение истина (Т), так и значение ложь (F), то оно называется выполнимым. Высказывания с таблицами истинности 2 - 7, 10, 11, 15 и 16 выполнимы.
Задание 7. Среди всех высказываний из заданий 5 и 6 указать все тавтологии и все выпол-нимые высказывания ■
Задание 8. Привестипример высказывания, которое не является выполнимым и не являет-ся тавтологией ■
Дата добавления: 2015-10-16; просмотров: 277 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Простые и составные высказывания | | | Логические рассуждения и их значимость |