Пути в графах

Как и в разделе 2, будем давать определения сразу для неориентированного и ориентиро-ванного случая, указывая отличия в скобках. Наиболее общим понятием является понятие пути (орпути). Путём (орпутём) в графе (орграфе) называется чередующаяся последовательность μ вершин и рёбер (дуг), начинающаяся и кончающаяся в вершинах:

μ = á v ₀, b ₁, v ₁, b ₂,..., v_{k -1}, b_k, v_k ñ, (4)

такая, что вершины v_i и v_{i +1} соединены ребром (дугой) b_k.

Вершина v ₀ называется началом пути (орпути) μ, вершина v_k – концом пути (орпути) μ, а число k, равное числу рёбер (дуг), входящих в путь (орпуть) – его длиной. Говорят также, что путь μ соединяет вершины v ₀ и v_k (орпуть μ ведёт из v ₀ в v_k). Обратным путём для пути μ на- зывается путь μ ^-1 = á v_k, b_k, v_{k -1}, b_{k -1},..., v ₁, b ₁, v ₀ñ. Другими словами, путь μ ^-1состоит из тех же самых вершин и рёбер, но проходимых в обратном порядке. Обратим внимание, что обратный путь определён только в неориентированном случае.

Цепью (орцепью) называется путь (орпуть), в котором все рёбра (дуги) различны. Прос-

Рис.7

Рис.8	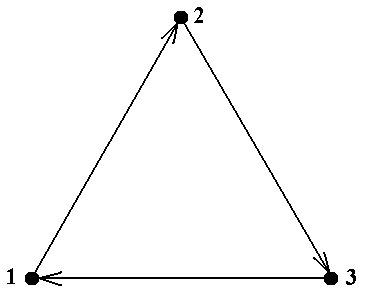Рис.9

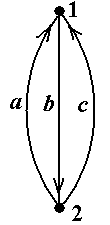
Рис. 10

той цепью (орцепью) называется цепь (орцепь), в которой все вершины различны. Путь (ор-путь), в котором начало и конец совпадают, называется циклическим путём (орпутём). Цик-лический путь, являющийся цепью (орцепью), называется циклом (орциклом). Цикл (орцикл), в котором все вершины, кроме начала и конца, различны и не совпадают с началом, называется простым циклом (орциклом).

Говорят, что не циклический путь ν содержится в не циклическом пути μ, если последова-тельность ν или последовательность ν ^-1 является подпоследовательностью последовательности μ. В ориентированном случае остаётся только часть этого определения: не циклический орпуть ν содержится в не циклическом пути орпути μ, если последовательность ν является подпоследо-вательностью последовательности μ.

Для циклических путей последнее определение требуется модифицировать, учитывая то, что такой путь можно «обходить», начиная с любой вершины, отчего он, конечно же, не изме-нится. Поэтому можно дать такие четыре определения:

1) не циклический путь ν содержится в циклическом пути μ, если последовательность μ можно циклически перенумеровать так, что последовательность ν или последовательность ν ^-1 станет подпоследовательностью этой перенумерованной последовательности μ;

2) не циклический орпуть ν содержится в циклическом орпути μ, если последовательность μ можноциклически перенумеровать так, что последовательность ν станет подпоследователь-ностью этой перенумерованной последовательности μ;

3) циклический путь ν содержится в пути μ, если последовательность ν или последова-тельность ν ^-1 можноциклически перенумеровать так, что эта перенумерованная последователь-ность ν станет подпоследовательностью последовательности μ;

4) циклический орпуть ν содержится в орпути μ, если последовательность ν можноцикли-чески перенумеровать так, что эта перенумерованная последовательность ν станет подпоследо-вательностью последовательности μ.

Эти на первый взгляд сложные понятия разъясняются далее (см. пример 13).

Все вышеприведённые в данном разделе понятия относятся к произвольным графам и ор-графам (см. раздел 1.1). В случае простых графов и орграфов понятие пути (орпути) упрощает-ся: под путём (орпутём) понимается последовательность вершин

μ =á v ₀, v ₁,..., v_{k -1}, v_k ñ, (5)

такая, что множество вершин { v_i, v_{i +1}} определяет ребро графа (петлю, если v_i и v_{i +1} совпадают)

(пара вершин á v_i, v_{i +1}ñ определяет дугу орграфа (петлю, если v_i и v_{i +1} совпадают)). Напомним, что в простых графах (орграфах) пара вершин однозначно определяет ребро (дугу), в то время как в графах общего вида таких рёбер (дуг) может быть несколько (см. рис.3, а также рис.5.1 и

10.1). Соответственно упрощаются все остальные приведённые выше определения – достаточно указывать только последовательности вершин.

Приведём примеры, иллюстрирующие и разъясняющие введённые понятия.

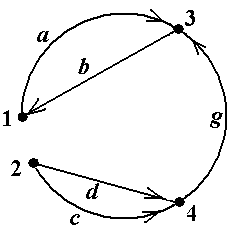
Пример 10. В графе, показанном на рис.11 (копия рис.5-6), обратным к пути μ = á1, f, 4, d, 2, c, 4, g, 3ñ является путь μ ^-1= á3, g, 4, c, 2, d, 4, f, 1ñ. Обратным к циклическому пути μ =á1, f, 4, d, 2, e, 3, b, 1ñ является циклический путь μ ^-1 = á1, b, 3, e, 2, d, 4, f, 1ñ (проверьте!) ■

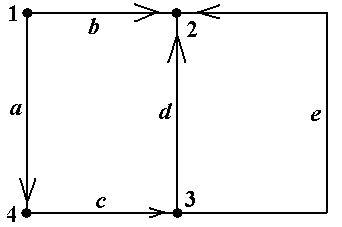
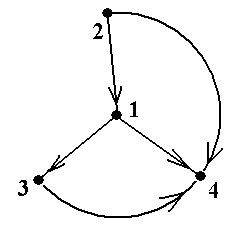
Пример 11. В графе, показанном на рис.12 (копия рис.5-7), обратным к простому пути μ = á2, 1, 4, 3ñ является путь простой путь μ ^-1 = á3, 4, 1, 2ñ. Обратным к циклическому пути μ ^-1 = á2, 4, 1, 3, 4, 2ñ является циклический путь μ ^-1 = á2, 4, 3, 1, 4, 2ñ ■

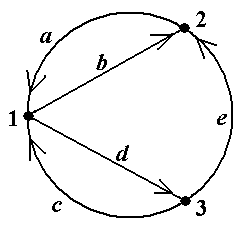
Пример 12. В графе, показанном на рис.13 (копия рис.5-3) последовательность μ = á1, d, 3,

e, 2, b, 1, a, 2, b, 1, c, 3ñ является путём с началом в вершине 1 и концом в вершине 3. Его длина, т.е. число входящих в него рёбер, равно 6. Этот путь не является цепью, так как не все его рёбра различны (ребро b встречается два раза). В этом же графе последовательность ν = á1, d, 3, e, 2, b, 1, c, 3ñ является цепью с началом в вершине 1 и концом в вершине 3. Эта цепь не является простой, так как в ней не все вершины различны (вершины 1 и 3 встречаются по два раза). По-следовательность λ = á1, d, 3ñ является простой цепью. Последовательность λ* = á1, c, 3ñ также является простой цепью, отличной от простой цепи λ = á1, d, 3ñ (см. рис.13). Заметим, что все четыре рассмотренных в примере пути μ, ν, λ, λ* соединяют одну и ту же пару вершин 1 и 3 ■

Пример 13. Граф, показанный на рис.14 (копия рис.7-c) является простым графом, поэто-му для задания путей можно пользоваться упрощёнными последовательностями, состоящими

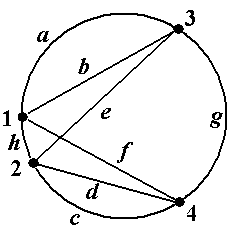Рис.11

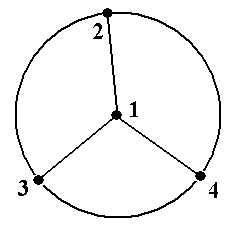Рис.12

только из вершин. Последовательность μ = á D, C, G, E, C, B, G, E, F ñ является путём с началом в

вершине D и концом в вершине F; его длина равна 8. Путь μ не является цепью, так как ребро { G, E } входит в него дважды. Последовательность ν = á D, C, G, E, C, B, F ñ является цепью, так как все её рёбра не повторяются (проверьте!), но она не является простой цепью, так как вершина C встречается в ней два раза. Последовательность λ = á D, C, B, F ñ является простой цепью, поскольку все её вершины различны. Заметим, что все три рассмотренные пути – μ, ν, λ – соединяют одну и ту же пару вершин D и F ■

Рис.13

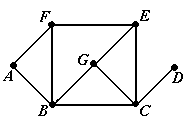Рис.14

Замечания в конце примеров 12 и 13 приводят к достаточно простому умозаключению, сформулированному в следующем утверждении.

Утверждение 6. Д ля всякого пути (орцепи), соединяющего две разные вершины, есть содержащаяся в нём цепь (орцепь), соединяющая те же две вершины. Для всякой цепи (орцепи), соединяющей две вершины, есть содержащаяся в ней простая цепь (орцепь), соединяющая те же две вершины ■

Заметим, что существующая в силу утверждения 6 цепь может совпадать с содержащим её путём (если сам путь уже является цепью); существующая в силу утверждения 6 простая цепь может совпадать с содержащей её цепью (если сама эта цепь уже является простой цепью).

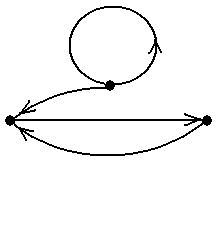
Пример 14. В графе, показанном на рис.15 (копия рис.5-15) последовательность μ = á1, a, 2, b, 1, a, 2ñ является путём. Этот путь не является цепью, поскольку он проходит два раза по ребру a. Двумя содержащимися в этом пути цепями являются только цепи ν = á1, a, 2ñ и ν * = á1, b, 2ñ. Обе эти цепи уже являются простыми, и поэтому любая содержащаяся в одной из них простая цепь совпадает с содержащей цепью ■

Заметим также, что во всех рассмотренных в примерах 12 − 14 путях начальная и конеч-ная вершины всегда различны, т.е. ни один из них не является циклическим путём.

Задание 4. Вграфах, показанных на рис.5, найти

1) путь, не являющийся цепью;

2) содержащуюся в найденном в 1) пути цепь, не являющуюся простой, соединяющую те же самые вершины;

3)содержащуюся в найденной в 2) цепи простую цепь, соединяющую те же самые верши-ны.

Если некоторые искомые объекты не существуют (как в примере 14), то объяснить это ■

Задание 5. Вграфах, показанных на рис.7, найти

1) путь, не являющийся цепью;

2) не содержащуюся в найденном в 1) пути цепь, не являющуюся простой;

3) не содержащуюся в найденной в 2) цепи простую цепь.

Если некоторые искомые объекты не существуют, то объяснить это ■

Пример 15. Рассмотрим простой граф, показанный на рис.16 (копия рис.5-9). Не цикли-

ческий путь μ = á6, 2, 5ñ содержится в циклическом пути ν = á2, 5, 3, 6, 2ñ, хотя последователь-ность μ не является подпоследовательностью последовательности ν. Действительно, если тот же самый циклический путь ν начать с вершины 6, т.е. записать в виде ν = á6, 2, 5, 3,6ñ, то после такой перенумерации последовательность μ становится подпоследовательностью последова-тельности ν. Рассмотрим теперь не циклический путь μ = á4, 1, 5ñ и циклический путь ν = á1, 4, 2, 5, 1ñ. Последовательность á4, 1, 5ñ не является подпоследовательностью ни самой последова-тельности ν,ни любой её циклической перестановки: á4, 2, 5, 1, 4ñ, á2, 5, 1, 4, 2ñ, á5, 1, 4, 2, 5ñ. Однако обратная последовательность μ ^-1= á5, 1, 4ñ содержится в циклически переставленной ν = á4, 2, 5, 1, 4ñ, и, значит, в силу введённых определений, путь μ = á4, 1, 5ñ содержится в цикли-ческом пути ν ■

Рис.15

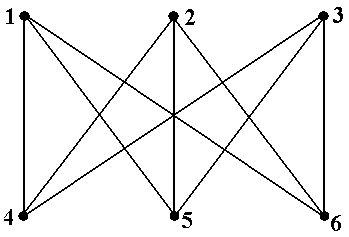Рис.16

Пример 16. В графе, показанном на рис.13, последовательность μ = á1, d, 3, е, 2, е, 3, с, 1, b, 2, a, 1ñ является циклическим путём, но не является циклом, поскольку ребро е входит в него дважды. Содержащийся в пути μ путь ν = á1, d, 3, с, 1, b, 2, a, 1ñ является циклом, но не является простым циклом, так начальная и конечная вершина 1 входит в него 3 раза, вместо двух, требу-емых определением. Наконец, содержащийся в пути ν путь λ = á1, d, 3, с, 1ñ является простым циклом ■

Пример 17. В графе, показанном на рис.14, последовательность μ = á E, C, G, B, A, F, B, G, E ñ является циклическим путём, но не является циклом, поскольку ребро { G, B } входит в него дважды. Содержащийся в пути μ путь ν = á E, C, B, A, F, B, G, E ñ является циклом, но не является простым циклом, так вершина B входит в него 2 раза. Наконец, содержащийся в пути ν путь λ = á E, C, B, G, E ñ является простым циклом ■

Имеет место утверждение, аналогичное утверждению 7 для не циклических путей.

Утверждение 7. Д ля всякого циклического пути (орпути) есть содержащийся в нём цикл (орцикл). Для всякого цикла (орцикла) есть содержащийся в нём простой цикл (орцикл) ■

Задание 6. Вграфах, показанных на рис.5, найти

1) циклический путь, не являющийся циклом;

2) содержащийся в найденном в 1) пути цикл, не являющийся простым;

3) содержащийся в найденном в 2) цикле простой цикл.

Если некоторые искомые объекты не существуют, то объяснить это ■

Задание 7. Вграфах, показанных на рис.7, найти

1) циклический путь, не являющийся циклом;

2) не содержащийся в найденном в 1) пути цикл, не являющийся простым;

3) не содержащийся в найденном в 2) цикле простой цикл.

Если некоторые искомые объекты не существуют, то объяснить это ■

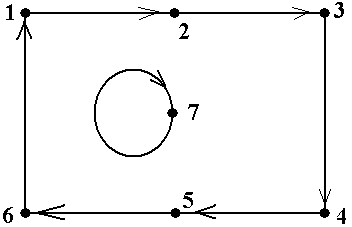
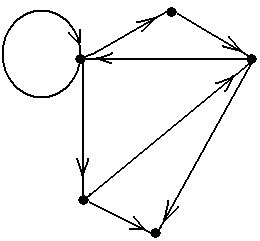
Пример 18. В орграфе, показанном на рис.17 (копия рис.10-3) последовательность μ = á1, b, 2, a, 1, d, 3, c, 1ñ является циклическим орпутём, который является орциклом. Этот орцикл содержит два простых цикла: ν ₁ = á1, b, 2, a, 1ñ и ν ₂ =á 1, d, 3, c, 1ñ. Кроме них, в данном орграфе есть простой орцикл á1, d, 3, e, 2, a, 1ñ ■

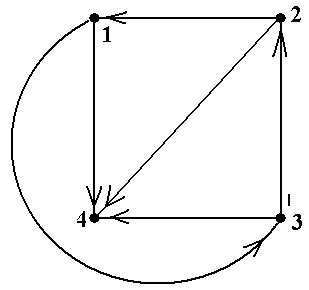
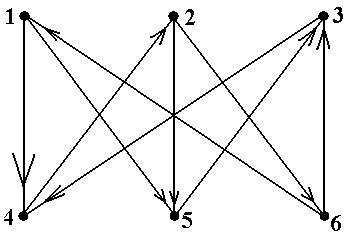
Пример 19. В орграфе, показанном на рис.18 (копия рис.10-4) имеется два орцикла: á1, 2, 3, 4, 5, 6, 1ñ и á7, 7ñ. Они оба являются простыми орциклами ■

Рис.17

Рис.18

Задание 8. Ворграфах, показанных на рис.10, найти

1) циклический орпуть, не являющийся орциклом;

2) содержащийся в найденном в 1) орпути орцикл, не являющийся простым;

3) содержащийся в найденном в 2) орцикле простой орцикл.

Если некоторые искомые объекты не существуют, то объяснить это ■

Задание 9. Ворграфах, показанных на рис.10, найти

1) циклический орпуть, не являющийся орциклом;

2) не содержащийся в найденном в 1) пути орцикл, не являющийся простым;

3) не содержащийся в найденном в 2) орцикле простой орцикл.

Если некоторые искомые объекты не существуют, то объяснить это ■

Введём ещё одно важное для дальнейшего понятие. Граф (орграф) называется ациклич-ным, если он не содержит циклов (орциклов). Рассмотрим подробнее ацикличные орграфы. В ацикличном орграфе по самому определению отсутствуют орциклы и, следовательно, все орпу-ти являются простыми. Однако для ацикличных орграфов верен и более специальный факт, в каком-то смысле описывающий их структуру. Имеет место

Утверждение 8. Пусть G (V, A) – простой ацикличный граф с множеством вершин V и множеством дуг A. Тогда множество вершин V разбивается на непересекающиеся подмножест-ва V ₁, …, V_m, такие, что для любой дуги (p, q) графа G начало p содержится в множестве V_i c бóльшим номером, чем конец q.

Доказательство этого утверждения, по сути, является алгоритмом построения указанных подмножеств. Поскольку граф ацикличен, то в нём найдётся хотя бы одна дуга, из которой не выходят дуги. Обозначим множество всех таких вершин через V ₁. Удалим из графа G все вер-шины из V ₁ и все ведущие в них дуги. Оставшийся граф также будет ацикличным. Множество его вершин, из которых не выходят дуги, обозначим через V ₂. Продолжая этот процесс, полу-чим разбиение с требуемыми свойствами (последний оставшийся граф G_m не может содержать дуг, иначе на нём процесс не мог бы окончиться) ■

Дата добавления: 2015-10-16