Связность и компоненты связности

Вершина j графа (орграфа) называется достижимой из вершины i, если существует путь (орпуть) с началом в i и концом в j. Множество K вершин графа (орграфа) называется компо-нентой связности (сильной связности), если любые две вершины из K взаимно достижимы, и при этом множество K является максимальным по включению множеством, обладающим дан-ным свойством (это означает, что при добавлении к K хотя бы одной новой вершины свойство взаимной достижимости теряется). Заметим, что множество, состоящее из одной вершины, яв-ляется связным (в орграфе – сильно связным) в «силу ложности посылки», но далеко не всегда является компонентой связности (сильной связности), поскольку не обязано быть максималь-ным по включению. Заметим также, что множество всех вершин графа (орграфа) также не обя-зано быть компонентой связности (сильной связности). Если же граф (орграф) состоит из един-ственной компоненты, то он называется связным (сильно связным).

Пример 20. Рассмотрим граф, показанный на рис.19 (копия рис.7-f). У него есть три ком-поненты связности: { A, B, C, D }, { E, F, G, H, I, J }, { R }■

Пример 21. Рассмотрим орграф, показанный на рис.20 (копия рис.10-6). В нём вершины 1 и 3 взаимно достижимы (с помощью дуг a и b), поэтому они по определению входят в одну и ту же компоненту сильной связности. Каждая из вершин 2 и 4 образует отдельную компоненту сильной связности, поскольку из 3 нельзя перейти в 4, а из 4 нельзя перейти в 2. Таким образом, у данного графа имеется три компоненты сильной связности: {1, 3}, {2} и {4}■

Задание 10. Найти компоненты связности в графах на рис.7 ■

Задание 11. Найти компоненты сильной связности в орграфах на рис.10 ■

Наличие нескольких кратных рёбер и любого числа петель, естественно, никак не сказы-вается на компонентах связности ни в неориентированном, ни в ориентированном случае. Поэ-тому в обоих случаях для нахождения компонент связности можно преобразовать граф к прос-тому графу без петель, оставив по одному ребру (дуге) среди нескольких кратных и удалив все петли.

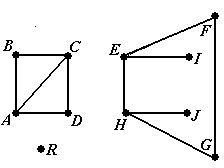Рис.19

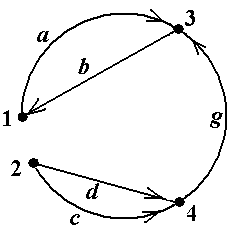Рис.20

Пример 22. Граф, показанный на рис.21a (копия рис.5-12), не является простым и содер-жит петлю при вершине. После удаления кратной дуги и петли (а также введения нумерации вершин) получается простой граф, показанный на рис.21b, в котором, как и в исходном графе, имеется одна компонента связности.

Рис.21a

Рис.21b

Пример 23. Орграф, показанный на рис.20, не является простым, поскольку дуги c и d кратны. После удаления одной из кратных дуг получается простой орграф, показанный на рис.22. В нём, как и в исходном орграфе, содержатся те же компоненты сильной связности: {1, 3}, {2} и {4}. Заметим, что дуги a и b в исходном орграфе не являются кратными, в отличие от дуг c и d ■

Рис.22

Задание 12. Привести все графы на рис.5, 7 и орграфы на рис.10, которые содержат крат-ные дуги и/или петли к простым графам (орграфам) без петель. В качестве ответов нарисовать пару «исходный-изменённый граф» и описать изменёный граф (орграф) парой á V, E ñ (á V, А ñ), как это делалось в примерах 4 – 6 ■

Компоненты связности (сильной связности) в небольших графах, показанных на рис.7 и 10, находятся непосредственно (как говорят, «глазами»). Надо сказать, что «глазами» выполня-лись и все предыдущие задания этой главы. Однако ведущую роль в решении прикладных задач дискретного характера играют алгоритмы. Конечно, алгоритмы для решения всех приведённых выше заданий хорошо известны. В этом разделе излагается алгоритм нахождения компонент связности неориентированных графов. Учитывая суть задания, можно обойтись простыми гра-фами без петель. Аналогичный алгоритм для орграфов здесь не излагается.

Прежде, чем перейти к формальным конструкциям, рассмотрим следующий

Пример 24. На рисунке 23 показан граф, содержащий 300 вершин и около 1200 рёбер. Число компонент связности в нём равно двум. Однако даже в данном, сравнительно простом, случае проверить это «глазами», мягко говоря, затруднительно ■

4.1. Алгоритм нахождения компонент связности простых неориентированных гра-фов. Когда речь заходит о каких бы то ни было алгоритмах, первым – и часто определяющим вопросом – является вопрос о формальном представлении рассматриваемых объектов или, как часто говорят, о выборе соответствующей структуры данных. В разделе 1.1 было дано формаль-ное представление простых неориентированных графов в виде пары á V, E ñ, где V = {1, 2, …, n } – множество вершин графа, E V *², где V *² – множество всех одно- и двухэлементных подмно-жеств множествавершин V. Двухэлементное множество { x, y }, принадлежащее E, интерпрети-руется как ребро с концами x и y.

Однако в данном случае, как и во многих других, более адекватной структурой данных яв-ляется следующая. Граф задаётся в виде массива, i -ый элемент которого соответствует вершине i. Сам же i -ый элемент является массивом, состоящим из номеров всех вершин, смежных с вер-

Рис.23

шиной i. В рамках такой структуры удобно просматривать все вершины, смежные с данной, чем и оправдано их применение. Такое представление графов назовём массивом смежных вершин.

Для орграфов аналогичное представление определяется как массив, i -ый элемент которого является массивом номеров всех вершин, в которые ведёт дуга из вершины i.

Пример 25. Для графа, показанного на рис.6, массив смежных вершин имеет следующий вид:

á á2, 4, 5ñ, á3, 4, 5ñ, á2, 4ñ, á2, 3, 5ñ, á1, 2, 4ñ ñ ■

Пример 26. Для графа, показанного на рис.24 (полученным из графа на рис.19 перенуме-рацией вершин), указанное представление имеет следующий вид: á á2, 3, 4ñ, á1, 3ñ, á1, 2, 4ñ, á1, 3ñ, á6, 8, 9ñ, á5, 7, 10ñ á6, 8ñ, á5, 7ñ, á5ñ, á6ñ, áñ ñ. Обратите внимание на последний (11-ый) массив: поскольку вершина 11 изолирована, список смежных с ней вершин пуст ■

Пример 27. Для графа, показанного на рис.25 (копия рис.10-5), указанное представление имеет следующий вид: á á3, 4ñ, á1, 4ñ, á2, 4ñ, áñ ñ. На 4-ой позиции стоит пустой кортеж, так как из вершины 4 не выходит ни одна дуга.

Задание 13. Все графы и орграфы, полученных в результате выполнения задания 12, пред-ставить в виде массива смежных вершин (см. примеры 25 – 27) ■

Рис.24

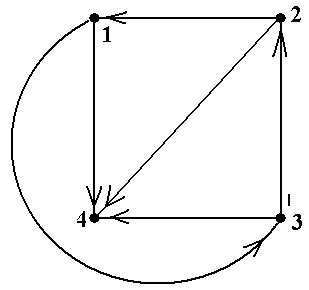Рис.25

Далее рассматривается основной материал данного раздела. Предлагается алгоритм, по массиву смежных вершин определяющий компоненты связности графа. Суть его такова. Опре-делим массив M длины n (через n обозначено число вершин графа). Присвоение i -ой вершине метки а означает формальную операцию присвоения M [ i ] = а. Начинаем с любой вершины (для определённости, с первой). Присваиваем ей метку -1.

Пусть некоторое множество вершин имеет метки -1 и +1. Возьмём любую вершину x с меткой -1 (если таковая найдётся) и у всех вершин, смежных с ней и ещё не имеющих метку, поставим метку -1. После этого, независимо от того, была ли помечена хотя бы одна вершина, у вершины x заменим метку -1 на +1. Если же ни одной вершины с меткой -1 не найдётся, то все вершины с меткой +1 образуют 1-ую компоненту связности. Если больше непомеченных вер-шин нет, то граф состоит из одной компоненты связности. Если есть хоть одна непомеченная вершина y, то пометим её меткой -2 и повторим весь процесс с заменой 1 на 2. Далее, если ещё остались непомеченные вершины, пометим любую из них меткой -3, и т.д, вплоть до того, когда все вершины становятся помеченными. При этом все вершины с одной и той же меткой i обра-зуют i -ую компоненту связности.

Пример 28. Применим описанный алгоритм для графа из примера 26 (рис.24). Для него массив смежных вершин таков: á á2, 3, 4ñ, á1, 3ñ, á1, 2, 4ñ, á1, 3ñ, á6, 8, 9ñ, á5, 7, 10ñ á6, 8ñ, á5, 7ñ, á5ñ, á6ñ, áñ ñ.

1. Инициализация. В данном случае число вершин равно 11. Поэтому определим массив M длины 11 и положим M [1] = -1.

2. В соответствии с алгоритмом положим M [2] = -1, M [3] = -1, M [4] = -1.

3. Поскольку помечены все вершины из списка смежных с вершиной 1 вершин 2, 3, 4, то

положим M [1] = 1.

4. Возьмём следующую вершину 2 с меткой -1. Смежные с ней вершины 1, 3 уже помече-ны. В соответствии с алгоритмом положим M [2] = 1.

5. Возьмём следующую вершину 3 с меткой -1. Смежные с ней вершины 1, 2, 4 уже поме-чены. В соответствии с алгоритмом положим M [3] = 1.

6. Возьмём следующую вершину 4 с меткой -1. Смежные с ней вершины 1, 3 уже помече-ны. В соответствии с алгоритмом положим M [4] = 1.

7. Поскольку более вершин с меткой -1 нет (M [1] = M [2] = M [3] = M [4] = 1), то выбираем следующую непомеченную вершину 5 и присваиваем ей метку M [5] = -2.

8. В соответствии с алгоритмом для смежных с вершиной 5 вершин 6, 8, 9 положим M [6] = -2, M [8] = -2, M [9] = -2.

9. Поскольку помечены все вершины из списка смежных с вершиной 5 вершин 6, 8, 9, то

положим M [5] = 2.

10. Возьмём следующую вершину 6 с меткой -2. Смежными с ней вершинами является 5 (уже помеченная), а также 7 и 10 (ещё непомеченные). В соответствии с алгоритмом положим M [7] = -2, M [10] = -2.

11. В соответствии с алгоритмом положим M [6] = 2.

12. Возьмём следующую вершину 7 с меткой -2. Смежными с ней вершинами является 6 и 8 (уже помеченные). В соответствии с алгоритмом положим M [7] = 2.

13. Возьмём следующую вершину 8 с меткой -2. Смежными с ней вершинами является 5 и (уже помеченные). В соответствии с алгоритмом положим M [8] = 2.

14. Возьмём следующую вершину 9 с меткой -2. Смежной с ней вершинами является только 5 (уже помеченная). В соответствии с алгоритмом положим M [9] = 2.

15. Возьмём следующую вершину 10 с меткой -2. Смежной с ней вершинами является только 6 (уже помеченная). В соответствии с алгоритмом положим M [10] = 2.

16. Поскольку вершин с меткой -2 нет (M [5] = M [6] = M [7] = M [8] = M [9] = M [10] = 2), то выбираем следующую непомеченную вершину 11 и присваиваем ей метку M [11] = -3.

17. В соответствии с алгоритмом просматриваем все вершины, смежные с 11. Поскольку вершин, смежных с 11, не существует, то меняем метку M [11]: M [11] = 3.

18. Поскольку более вершин с меткой -3 не существует, то в соответствии с алгоритмом ищем непомеченную вершину. Так как таковых не имеется, то алгоритм останавливается.

После остановки имеем следующий массив M: M = á1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3ñ. Это и означает, что 1-ую компоненту связности образуют вершины 1, 2, 3, 4; 2-ую компоненту связности – вершины 5, 6, 7, 8, 9, 10; 3-ью компоненту связности – изолированная вершина 11■

Задание 14. Для всех неориентированных графов, рассмотренных в задании 13, найти указанным алгоритмом компоненты связности (см. пример 28) ■

Дата добавления: 2015-10-16