Эйлеровы циклы

5.1. Кёнигсбергские мосты. Не каждому городу выпадает честь быть отмеченным в та-кой точной науке, как классическая математика. Кёнигсберг же благодаря своим мостам и вели-кому учёному-математику XVIII-го века Леонарду Эйлеру вошёл в число математических зна-менитостей.

Рис.26. Великий математик Леонард Эйлер (1707 – 1783)

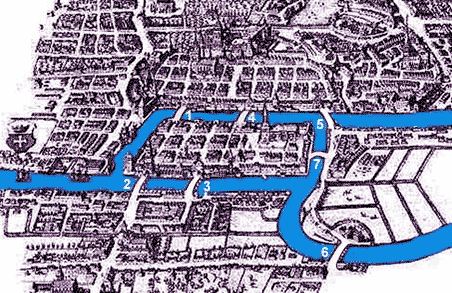Рис.27. Кенигсберг начала XVIII века с мостами

Леонард Эйлер (Leonhard Euler) родился 15 апреля 1707 г. в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и учёные, не желавшие тратить дорогое рабочее вре-мя на частые в других странах гражданские смуты и религиозные распри. Так переселилась в Базель из Голландии и семья Бернулли, давшая миру уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. Семья небогатого протестантского пастора Пауля Эй-лера жила в доме Бернулли. Иоганн Бернулли быстро заметил и оценил талант Леонарда, стал его наставником, а сыновья Иоганна Николай и Даниил – его друзьями.

Более всего поражает способность великого учёного говорить о сложных вещах простым языком. Для решения серьёзных математических задач Эйлер использовал наглядные голово-ломки. Одна из них положила начало совершенно новой области исследований, выросшей впос-ледствии в самостоятельный раздел математики – теорию графов. Особенность этой теории – в геометрическом подходе к изучению объектов. Живя в Кёнигсберге, прогуливаясь по его набе-режным, Эйлер обратил внимание на оригинальное расположение семи мостов города. Причи-ной этому было причудливое течение рукавов Прегеля, соединенных протокой, охватывающих с севера и юга остров Кнайпхоф, а затем сливающихся вместе (рис.27). Эти мосты назывались так:

1. Kramer-Brucke (Лавочный мост)

2. Grune Brucke (Зелёный мост)

3. Kottel-Brucke (Потроховый мост)

4. Schmiede-Brucke (Кузнечный мост)

5. Holz-Brucke (Деревянный мост)

6. Hohe-Brucke (Высокий мост)

7. Honig-Brucke (Медовый мост)

В 1736 Эйлер решил задачу, известную с тех пор как задача о кенигсбергских мостах:можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. На рис.28 изображена условная схема семи мостов Кё-нигсберга (заметим, что сейчас осталось только два из них).

Упростим схему, показанную на рис.28. Для этого представим каждый из четырёх участ-ков суши одной точкой, а каждый из мостов – линией, соединяющей соответствующие точки. В результате получаем граф, показанный на рис.3. Обратим внимание на то, что данный граф не

Рис.28

является простым (см. пример 2). Нетрудно понять, что исходная задача стала значительно бо-лее обозримой. В уже введённых терминах (см. раздел 4) вопрос ставится так: существует ли в графе на рис.3 цикл, проходящий по всем рёбрам? Напомним, что однократность прохождения каждого ребра включена в определение цикла в разделе 4. Эйлер дал общий ответ на поставлен-ный вопрос в следующем виде.

Теорема. Для того чтобы данный связный граф имел цикл, проходящий по всем рёбрам, необходимо и достаточно, чтобы степени всех вершин графа были чётными. Для того чтобы данный связный граф имел цепь между вершинами А и В, проходящую по всем рёбрам, необхо-димо и достаточно, чтобы степени всех вершин, кроме А и В, были чётными, а степени этих вершин были нечётными.

Поскольку в графе на рис.3 степени некоторых вершин нечётны, то, следовательно, требу-емого цикла не существует. В честь Эйлера циклы в неориентированных графах, проходящие по всем рёбрам, были названы эйлеровыми циклами, как и соответствующие цепи.

5.2. Алгоритм Флёри. Теорема Эйлера сама по себе является теоремой существования: в ней не говорится о том, как построить эйлеров цикл. Эффективный алгоритм был предложен французским математиком Флёри в 1873 году – почти через 150 лет после открытия Эйлера. Для его изложения нам понадобится важное понятие перешейкав графе. Перешеек – это ребро, удаление которого разделяет связную компоненту графа на две несвязные части.

Пример 29. Найдём все перешейки в графе, показанном на рис.29 a. Граф состоит только из одной компоненты связности, так что надо найти каждое ребро, удаление которого делает граф несвязным.

Рис.29

Ребро {3, 5} является перешейком; его удаление делает граф несвязным, как показано на рис. 29 b. Ребро {7, 8} также является перешейком; его удаление делает граф несвязным, как показа-но на рис.29 c; при этом вершина 8 образует отдельную компоненту связности. Удаление ребра {6, 7} не приводит к разделению графа, как показано на рис.29 d; то же самое относится к удалению любого ребра (кроме {3, 5}и {7, 8}).

Дата добавления: 2015-10-16