Понятие и определения графа

Во многих случаях жизни привычка толкает нас рисовать на бумаге точки, изображающие населенные пункты, агрегаты, людей, химические вещества и т.д., и соединять эти точки линия-ми или стрелками, указывающими на связи между соответствующими объектами. Такие схемы встречаются всюду под разными названиями: карты дорог, технологические схемы предприя-тий, диаграммы организаций, электрические цепи, сети коммуникаций, блок-схемы алгоритмов, генеалогические деревья и пр. Хотя такого рода объекты изучались достаточно давно (начиная с Эйлера), немецкий математик Д. Кёниг был первым, кто предложил называть такие схемы «графами» и систематически изучать их свойства (в 1936 году).

Граф характеризует связи между объектами; условно эти объекты изображаются точками, а связи между ними – линиями, соединяющими соответствующие точки. При этом положение точек, наклон и длина линий совершенно не имеют значения (в отличие, например, от изобра-жений в геометрии); важно лишь то, какие именно пары точек соединены, а какие – нет. Для удобства будем обозначать вершины натуральными числами (вообще говоря, их можно обозна-чать любыми символами).

Пример 1. На рис.1 приведен пример трёх графов. На первый взгляд эти графы различны. Однако на самом деле во всех трёх случаях изображен один и тот же граф. Действительно, во всех трех изображениях соединены между собой те же самые пары точек: {1, 2}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {4, 5}; никакие другие пары точек не соединены ■

Рис.1

В одних случаях при описании связей между объектами «направление» связи не имеет значения. Соответствующие точки в графе соединяются линией без стрелки (как на рис.1); граф в этом случае называется неориентированным. В других случаях важно не только то, что объек-ты связаны, но и то, как именно «направлена» эта связь. Соответствующие точки в графе соеди-няются линией со стрелкой; граф в этом случае называется ориентированным. С помощью нео-риентированных графов удобно представлять, например, карты дорог; технологические схемы естественно описывать с помощью ориентированных графов. Пример ориентированного графа (так называемая «сеть питания») показан на рис.2.

1.1. Формальное определение графов. Нам понадобятся введённые в разделе 3.5 понятия функции типа A → B, инъективной функции, множеств отправления, прибытия, определения и значения функции, а также введённое в разделе 3.1 понятия кортежа (пары и тройки).

Рис.2

1.1.1. Определение неориентированных графов. Обозначим через X *² множество всех одно- и двухэлементных подмножеств множества X. Дадим теперь необходимые формальные определения. Неориентированным графом G называется тройка á V, E, F ñ, где V – множество вершин графа, E – множество его рёбер, F – всюду определённая функция типа E → V *² (т.е. функция, у которой область определения совпадает с областью отправления). Это определение может показаться сложным и запутанным, особенно в сравнении с интуитивно ясным представ-лением о графе, данном в примере 1. Остановимся на этом подробнее.

Пример 2. Рассмотрим граф, показанный на рис.3. В этом графе множество рёбер E = { a, b, c, d, e, f, g }; множество вершин V = {1, 2, 3, 4}; V *² = {{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}. Рёбра a и b соединяют одни и те же вершины 1 и 3; рёбра c и d соединяют

одни и те же вершины 1 и 4; ребро e соединяет вершины 2 и 3; ребро f соединяет вершины 1 и 2; наконец, ребро g соединяет вершины 2 и 4. Именно такого рода соответствия формализуются с помощью функции F. В данном случае

F (a) = F (b) = {1, 3}, F (c) = F (d) = {1, 4}, F (f) = {1, 2}, F (e) = {1, 3}, F (g) = {2, 4}. (1)

Рёбра, соединяющие одну и ту же пару вершин, называются кратными. В рассматриваемом случае кратными являются рёбра a и b, а также c и d. Заметим, что концы определены для всех рёбер, что и означает, что функция F всюду определена. Другими словами, никаких «болтаю-щихся» концов у рёбер нет ■

В общем случае можно сказать, что значение функции F на произвольном ребре p, т.е. од-но- или двухэлементное множество вершин, как раз представляет собой множество концов дан-ного ребра p (сравните рис.3 и соотношения (1) и убедитесь в этом!). В примере 2 все эти множества были двухэлементными, т.е. рёбра, у которых оба конца совпадают, в графе на рис.3 отсутствуют. Однако в общем случае такие рёбра могут присутствовать.

Пример 3. Рассмотрим граф, показанный на рис.4. В этом графе F (a) = {1}, F (b) = {1, 2}. Рёбра, у которых концы совпадают (с вершиной A), называются петлями при вершинах (вер-шине A). Вообще говоря, петель при одной и той же вершине (т.е. кратных петель) может быть несколько, как и рёбер, соединяющих одну и ту же пару разных вершин ■

Рис.3

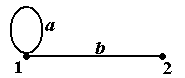Рис.4

Во многих случаях разным рёбрам графа соответствуют разные пары вершин (если они не являются петлями) и разные вершины (если они являются петлями). В этих случаях функция F является инъекцией (см. раздел 1.5), а соответствующий граф называется простым.

Напомним, что инъективной функцией, или инъекцией, называется функция F, такая, что

[ x ≠ y ] → [ F (x) ≠ F (y)] (2)

(определение импликации P → Q см. в разделе 1.2).

Поскольку каждое ребро простого графа однозначно определяется своими концами, то та-кое ребро можно однозначно задать двухэлементным или одноэлементным (для петли) множес-твом его концов. Таким образом, можно дать следующее формальное определение. Неориенти-рованным простым графом G называется пара á V, E ñ, где V – множество вершин графа, E V *² – множество его рёбер. Здесь одноэлементное множество из V, т.е. множество вида { i }, означает ребро – петлю при вершине i, а двухэлементное множество { i, j } означает ребро с концами i и j. Заметим также, что иногда в литературе простые графы называются графами, а графы, содержа-щие кратные рёбра – мультиграфами.

Пример 4. Рассмотрим граф, показанный на рис.4. Этот граф является простым. Поэтому его можно задать парой множеств á V, E ñ, где V = {1, 2} – множество вершин графа, E = {{1}, {1, 2}} – множество его рёбер ■

Пример 5. Граф, показанный на рис.1, является простым графом без петель. Он задаётся парой множеств á V, E ñ, где V = {1, 2, 3, 4, 5} – множество его вершин, E = {{1, 2}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {4, 5}} – множество его рёбер ■

Поскольку простой граф – частный случай графа, то введённое выше задание графа в виде тройки á V, E, F ñ является более общим и может быть использовано во всех случаях, в том числе и для простых графов. В то же время задание парой á V, E ñ, которое применимо ко всем простым парам, не может использоваться в общем случае: если несколько рёбер имеют общие концы i и j, то их, конечно, нельзя задать одним и тем же двухэлементным множеством { i, j }. Следует сказать, что задание парой проще, чем задание тройкой. Поэтому во всех случаях, когда это возможно, т.е. для простых графов, будем использовать задание парой á V, E ñ.

Резюмируем рассмотренные примеры 1 – 5.

Граф на рис.1 задаётся парой á V, E ñ, где V = {1, 2, 3, 4, 5}, E = {{1, 2}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {4, 5}}.

Граф на рис.3 задаётся тройкой á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d, e, f, g }, F (a) = F (b) = {1, 3}, F (c) = F (d) = {1, 4}, F (f) = {1, 2}, F (e) = {1, 3}, F (g) = {2, 4}.

Граф на рис.4 может быть задан как парой á V, E ñ, где V = {1, 2}, E = {{1}, {1, 2}}, так и тройкой á V, E, F ñ, где V = {1, 2}, E ={ a, b }, F (a) = {1}, F (b) = {1, 2}.

В связи с введёнными способами задания графов (напомним, что пока рассматриваются только неориентированные графы) предлагаются следующие виды стандартных заданий:

1) по заданному формальному описанию (в виде тройки или пары) нарисовать граф;

2) по заданному изображению дать формальное описание графа в виде пары á V, E ñ (если граф простой) или тройки á V, E, F ñ (в противном случае). Если номера вершин и/или имена рёбер на рисунке не указаны, дать их самостоятельно.

Задание 1а. По заданному формальному описанию нарисовать граф (см. примеры 1 – 5).

1. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d, e, f, g, h }, F (a) = F (b) = {1, 3}, F (c) = F (d) = {2, 4}, F (e) = {2, 3}, F (f) = {1, 4}, F (g) = {3, 4}, F (h) = {1, 2}.

2. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {2, 3}, {3, 4}, {1, 4}, {2, 4}}.

3. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e, f }, F (a) = F (b) = {1, 2}, F (c) = F (d) = {1, 3}, F (e) = F (f) = {2, 3}.

4. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e }, F (a) = F (b) = {1, 2}, F (c) = F (d) = {1, 3}, F (e) = {2, 3}.

5. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}.

6. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6}, E = {{2}, {6}, {1, 4}, {1, 5}, {1, 6}, {2, 5}, {3, 5}, {3, 6}}.

7. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c }, F (a) = F (b) = {1, 2}, F (c) = {3, 4}.

8. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6, 7}, E = {{7}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}, {1, 6}}.

9. G = á V, E ñ, где V = {1, 2, 3, 4, 5}, E = {{5}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {1, 5}}.

10. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e }, F (a) = F (b) = {1, 2}, F (c) = {1, 3}, F (d) = {2, 3}, F (e) = {3}.

11. G = á V, E, F ñ, где V = {1, 2}, E ={ a, b, c }, F (a) = F (b) = F (c) = {1, 2}.

12. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {2, 3}, {3, 4}, {1, 4}, {2, 4}, {1, 3}}.

13. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6}, E = {{1, 4}, {1, 5}, {1, 6}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}}.

14. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d }, F (a) = F (b) = {1, 3}, F (c) = {1, 4}, F (d) = {2, 3}.

15. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d, e }, F (a) = {1, 4}, F (b) = {1, 2}, F (c) = {3, 4}, F (d) = F (e) {2, 3} ■

Задание 1b. Графы, показанные на рис.5, задать парами á V, E ñ или тройками á V, E, F ñ (примеры 1 – 5) ■

Конечно, существует много других способов формального задания графов. В основном выбор формального задания графа (структуры данных) определяется эффективностью алгорит-ма, при программной реализации которого этот вид задания используется. Подробнее эти воп-росы рассматриваются в курсе САОД (Структуры и алгоритмы обработки данных).

1.1.2. Определение ориентированных графов. Оно во многом схоже с определением неориентированных графов. Ориентированным графом G называется тройка á V, A, F ñ, где V – множество вершин графа, А – множество его дуг, F – всюду определённая функция типа А → V ² (напомним, что через V ² обозначается прямое произведение множества вершин V на себя или V × V, т.е. множество всех пар á x, y ñ, где x, y Î V). Смысл этого определения такой же, как и для неориентированных графов. Именно, F (a) = á i, j ñ означает, что дуга a выходит из вершины i и входит в вершину j; если же i = j, то это означает, что данная дуга является петлёй при вершине i. Как и в неориентированном случае, если функция F инъективна, то соответствующий граф называется простым; при этом для каждой пары вершин á i, j ñ существует не более одной дуги с началом i и концом j. Поэтому здесь также можно задавать любую дугу как упорядоченную пару её концов á i, j ñ и записывать граф G в виде пары á V, A ñ, где множество дуг A V ².

Для сокращения записи иногда (если это не вызовет недоразумений) неориентированные графы будем называть просто графами, а ориентированные – орграфами.

Пример 6. Граф на рис.2 является простым орграфом без петель. Занумеруем его верши-ны так: Лисы – 1; Насекомые – 2; Трава – 3; Олени – 4; Птицы – 5. Тогда G = á V, A ñ, где V = {1, 2, 3, 4, 5}, А = {á1, 2ñ, á1, 5ñ, á2, 3ñ, á4, 3ñ, á5, 2ñ, á5, 3ñ} ■

---

Дата добавления: 2015-10-16