Рекуррентные соотношения, соответствующие им рекуррентные уравнения и их решения. Понятие характеристического многочлена.

Линейной рекуррентной последовательностью (линейной рекуррентой) называется всякая числовая рекуррентная последовательность , задаваемая линейным рекуррентным соотношением:

при

с заданными начальными членами , где n — фиксированное натуральное число, — заданные числовые коэффициенты, . При этом число n называется порядком последовательности.

Линейные рекуррентные последовательности иногда называют также возвратными последовательностями.

Для линейных рекуррентных последовательностей существует формула, выражающая общий член последовательности через корни её характеристического многочлена

Для чисел Фибоначчи такой формулой является формула Бине.

Пример

Для последовательности , удовлетворяющей линейному рекуррентному уравнению второго порядка с начальными значениями , , справедлива формула:

.

Для того, чтобы найти необходимо решить характеристическое уравнение . Если дискриминант этого уравнения отличен от нуля, то

где — любой из двух корней этого уравнения. Если же дискриминант характеристического уравнения равен нулю, то

В частности, для последовательности, определяемой следующим линейным рекуррентным уравнением второго порядка

; , .

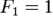корнями характеристического уравнения являются , . Поэтому

.

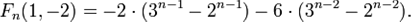Окончательно:

Дата добавления: 2015-09-06