Принцип включения и исключения и его применение к решению комбинаторных задач на примере задачи о беспорядках.

Классический пример использования формулы включений-исключений — задача о беспорядках. Требуется найти число перестановок множества таких что 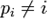для всех . Такие перестановки называются беспорядками.

Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа 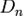беспорядков:

Это соотношение можно преобразовать к виду

Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:

Дата добавления: 2015-09-06