Отношения частичного порядка. Линейно- упорядоченные множества. Максим.(миним.) наимен(наибольш.) элементы частично упорядоченного множества и их свойства.

Частично упорядоченное множество — математическое понятие, которое формализует интуитивные идеи упорядочивания, расположения в определенной последовательности и т. п. Неформально говоря, множество частично упорядочено, если указано, какие элементы следуют (больше и т. п.) за какими. При этом в общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».

В качестве абстрактного примера можно привести совокупность подмножеств множества из трех элементов { x, y, z } (булеанданного множества), упорядоченное по отношению включения.

В качестве примера строгого частичного порядка «из жизни» можно привести множество людей, упорядоченное по отношению «быть предком».

Порядком, или частичным порядком, на множестве M называется бинарное отношение 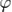на M (определяемое некоторым множеством 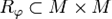), удовлетворяющее следующим условиям:

• Рефлексивность: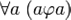

• Транзитивность:

• Антисимметричность: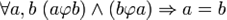

Множество M, на котором задано отношение частичного порядка, называется частично упорядоченным (англ. partially ordered set, poset). 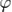Если быть совсем точным0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%BE_%D1%83%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D1%87%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE"[2], то частично упорядоченным множеством называется пара , где M — множество, а — отношение частичного порядка на M.

Отношение частичного порядка обычно обозначают символом , по аналогии с отношением «меньше либо равно» на множестве действительных чисел. При этом, если 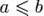, то говорят, что элемент a не превосходит b, или что a подчинен b.

Есл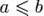и и 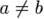, то пишут a < b, и говорят, что a меньше b, или что a строго подчинен b.

Иногда, чтобы отличить произвольный порядок на некотором множестве от известного отношения «меньше либо равно» на множестве действительных чисел, вместо и <используют специальные символы и соответственно.

Отношение, удовлетворяющее условиям рефлексивности, транзитивности и антисимметричности, также называют нестрогим, или рефлексивным порядком. Если условие рефлексивности заменить на условие антирефлексивности:

то получим определение строгого, или антирефлексивного порядка.

Если — нестрогий порядок на множестве M, то отношение <, определяемое как:

является строгим порядком на M. Обратно, если < — строгий порядок, то отношение , определенное как

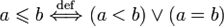
является нестрогим порядком.

Поэтому все равно — задать на множестве нестрогий порядок, или строгий порядок. В результате получится одна и та же структура. Разница только в терминологии и обозначениях.

Из-за того, что в частично упорядоченном множестве могут быть пары несравнимых элементов, вводятся два различных определения: минимального элемента и наименьшего элемента.

Элемент называется минимальным (англ. minimal element), если не существует элемента b < a. Другими словами, a — минимальный элемент, если для любого элемента либо b > a, либо b = a, либо b и a несравнимы. Элемент a называется наименьшим (0%90%D0%BD%D0%B3%D0%BB%D0%B8%D0%B9%D1%81%D0%BA%D0%B8%D0%B9_%D1%8F%D0%B7%D1%8B%D0%BA"англ. least element, lower bound (opp. upper bound)), если для любого элемента имеет место неравенство 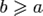. Очевидно, всякий наименьший элемент является также минимальным, но обратное в общем случае неверно: минимальный элемент a может и не быть наименьшим, если существуют элементы b, не сравнимые с a.

Очевидно, что если в множестве существует наименьший элемент, то он единственен. А вот минимальных элементов может быть несколько. В качестве примера рассмотрим множество натуральных чисел без единицы, упорядоченное по отношению делимости . Здесь минимальными элементами будут простые числа, а вот наименьшего элемента не существует.

Дата добавления: 2015-09-06