Степени матрицы

Если A — матрица смежности графа G, то матрица A^m обладает следующим свойством: элемент в i -й строке, j -м столбце равен числу путей из i -й вершины в j -ю, состоящих из ровно m ребер.

№25(устный)

№26 Компоненты связанности графа. Понятие дерева.

Дерево — это 0%A1%D0%B2%D1%8F%D0%B7%D0%BD%D1%8B%D0%B9_%D0%B3%D1%80%D0%B0%D1%84"связный 0%90%D1%86%D0%B8%D0%BA%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B3%D1%80%D0%B0%D1%84"ациклический 0%93%D1%80%D0%B0%D1%84_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"граф (то есть граф, не содержащий циклов, между любой парой вершин которого существует ровно один путь).0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_(%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2)"[1]

Ориентированное (направленное) дерево — ацикличный орграф (0%9E%D1%80%D0%B8%D0%B5%D0%BD%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B3%D1%80%D0%B0%D1%84"ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями. 0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_(%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2)"[2]

Формально дерево определяется как конечное множество T одного или более узлов со следующими свойствами:

• существует один корень дерева T

• остальные узлы (за исключением корня) распределены среди 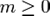непересекающихся множеств T ₁,..., T_m, и каждое из множеств является деревом; деревья T ₁,..., T_m называются поддеревьями данного корня T

Число различных деревьев, которые можно построить на n нумерованных вершинах, равно n^{n − 2} (Теорема 0 % 9 A%D 1 % 8 D%D 0 %BB%D 0 %B 8,_%D 0 %90%D 1 %80%D 1 %82%D 1 %83%D 1 %80"КэлиHYPERLINK "http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_(%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2)"[3]).

Производящая функция

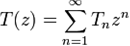
для числа T_n неизоморфных корневых деревьев с n вершинами удовлетворяет функциональному уравнению

.

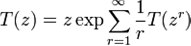Производящая функция

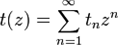
для числа t_n неизоморфных деревьев с n вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:

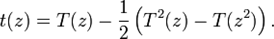
При 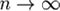верна следующая асимптотика

t_n ∼ C α ⁿ / n ^{5 / 2}

где C и α определённые константы, C = 0,534948..., α = 2,95576....

Дерево можно кодировать наборами из нулей и единиц. Рассмотрим, например, укладку дерева на плоскости. Начиная с какой либо вершины, будем двигаться по ребрам дерева, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах дерева. Проходя по некоторому ребру, записываем 0 при движении по ребру в первый раз и 1 при движении по ребру второй раз (в обратном направлении). Если m — число рёбер дерева, то через 2 m шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из 0 и 1 (код дерева) длины 2 m позволяет однозначно восстанавливать не только само дерево D, но и его укладку на плоскости. Произвольному дереву соответствуют несколько таких кодов. В частности, из этого способа кодирования вытекает следующая грубая оценка на число деревьев с n вершинами:

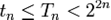
Дата добавления: 2015-09-06