Полные, двудольные и полные двудольные графы.

Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n (n − 1) / 2рёбер и обозначается K_n. Является регулярным графом степени n − 1.

Графы с K ₁ по K ₄ являются планарными. Полные графы с большим количеством вершин не являются планарными, так как содержат подграф K ₅ и, следовательно, не удовлетворяют критерию Понтрягина-Куратовского.

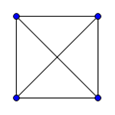
Ниже приведены полные графы с числом вершин от 1 до 8 и количества их рёбер.

K 1: 0	K 2: 1	K 3: 3	K 4: 6
K 5: 10	K 6: 15	K 7: 21	K 8: 28

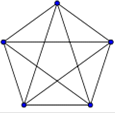
Двудо́льный граф или бигра́ф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Для того, чтобы проверить граф на предмет двудольности, достаточно в каждой компоненте связности выбрать любую вершину и помечать оставшиеся вершины во время обхода графа (например, поиском в ширину или в глубину) поочерёдно как чётные и нечётные (см. иллюстрацию). Если при этом не возникнет конфликта, все чётные вершины образуют множество U, а все нечётные — V.

№34 Планарные графы.

Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.

№38 Сформулировать теорему Понтрягина - Куратовского

Граф планарен тогда и только тогда, когда он не содержит подграфов, 0%93%D0%BE%D0%BC%D0%B5%D0%BE%D0%BC%D0%BE%D1%80%D1%84%D0%B8%D0%B7%D0%BC_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2&action=edit&redlink=1"гомеоморфных полному графу из пяти вершин (K ₅) или графу «домики и колодцы» (K _3,3).

№39 Понятие сети и потока в ней.

В теории графов транспортная сеть — ориентированный граф G = (V, E), в котором каждое ребро 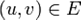имеет неотрицательную пропускную способность и поток f (u, v). Выделяются две вершины: источник s и сток t такие, что любая другая вершина сети лежит на пути из s в t. Транспортная сеть может быть использована для моделирования, например, дорожного трафика.

Целочисленная транспортная сеть — транспортная сеть, все пропускные способности ребер которой — целые числа.

Транспортная сеть (flow network) — ориентированный граф в котором

• каждому ребру приписана неотрицательная пропускная способность . Если , то .

• выделены две вершины: источник (source) s и сток (sink) t, такие, что любая другая вершина сети лежит на пути из s в t.

Поток (flow) — функция со следующими свойствами для любых вершин 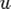и :

• Ограничение пропускной способности (capacity constraints). Поток не может превысить пропускную способность:

• Антисимметричность (skew symmetry). Поток из 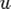в должен быть противоположным потоку из в :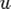

• Сохранение потока (flow conservation): для всех , кроме источника и стока.

' Величиной потока (value of flow) называется сумма потоков из источника . В дальнейшем мы докажем, что она равна сумме потоков в сток .

Задача о максимальном потоке (maximum flow problem): найти поток f такой, что величина потока максимальна.

Разрез (s-t cut) — разбиение множества всех вершин V на два подмножества, A и B, таких что , .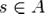

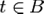Пропускная способность разреза (A,B) (the capacity of an s-t cut (A,B)) — сумма пропускных способностей всех рёбер из A в B .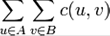

Поток через разрез (A,B) — сумма всех потоков из A в B . Он не превышает пропускную способность разреза, поскольку .

Минимальный разрез - разрез с минимальной пропускной способностью.

Остаточная пропускная способность (residual capacity) ребра 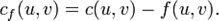Она всегда неотрицательна из-за условия на ограничение пропускной способности.

Остаточная сеть (residual network) Здесь - множество рёбер с положительной остаточной пропускной способностью. В остаточной сети может быть ребро из 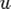в , даже если его нет в исходной сети. Это выполняется, когда в исходной сети есть обратное ребро (v, u) и поток по нему положителен.

Увеличивающий (остаточный, дополняющий) путь (augmenting path) — это путь в остаточной сети, где 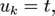и Можно доказать, что поток максимален тогда и только тогда, когда нет увеличивающего пути в остаточной сети.

Дата добавления: 2015-09-06