Цепи и антицепи, и их свойства.

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов a и b имеет место 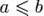или .

Важнейший частный случай линейно упорядоченных множеств ― вполне упорядоченные множества.

Формулировка теоремы Дилуорса

Пусть n — наибольшее количество элементов антицепи (англ. antichain) данного конечного частично упорядоченного множества M. Тогда M можно разбить на n попарно непересекающихся цепей.

Другими словами, минимальное число непересекающихся цепей, которые в совокупности содержат все элементы частично упорядоченного множества M, равно максимально возможному числу элементов в подмножестве множества M, состоящем из попарно несравнимых элементов, если это число конечно.

Булевы кубы и их характеристики. Расстояние между его элементами и их нумерация. Код Гроя.

В={0,1}

n-мерный булев куб — это множество Bⁿ (с заданным частичным порядком)

Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bn.

Дата добавления: 2015-09-06