Множества и действия над ними. Свойства операций над множествами.

Множество - Одно из основных и сходных понятий математики. множество состои из элементов. если элемент а принадлежит множеству М, это записывается как 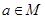, иначе как 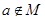или .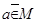

Множество А называется подмножеством М если всякий элемент А является элементом М. обозначается 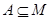.при этом говорят, что М содержит или покрывает А.

Множества А и М равны, если их элементы совпадают. Или, в формульном виде, соледующие две записи верны: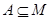

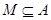
Есл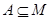и и 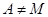, то А называется собственным, строгим или истиным подмножеством М и можно обозначить как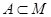

Множество бывают конечные и бесконечные.

Мощность множества - это количество его элементов. обозночается | M |

множество мощности 0 называется пустым

множество задаются разными способами:

1) списком (A ={1,2,3,4})

2) Порождающей процедурой(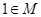, если 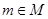то 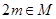(или иным другим способом, указывающим процедуру и необходимые данные для её подсчёта))

3) описанием свойств оего элементов (M - множество целых степеней двойки)

Действия над множествами

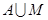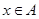Объединение множеств - множество, включающее в себя все элементы множества А и множества М. Обозначается . Условно можно записать как если или . объединение N множеств - аналогично.

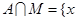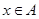Пересечение множеств А и М - множество, содержащее всебе элементы, присутствующие и в А и в М. Обозначается если и

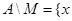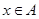разность множеств А и М - множество только тех элементов, которые есть в А но отсутствуют в М. Обозначается если и 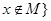. Если А\В= 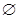(пустое множество), то 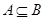. от перемены мест множеств результат меняется! Известна как операция дополнения A до U.

Симметричная разность множеств А и М - Множество, состоящее из элементов, существующих тольков в одном из данных множеств. обозначается А М ={x если x }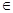

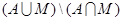Прямое произведение А и М - множество, состоящие из пар (a,m) таких, что 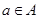и 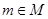. обозначается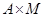

Операции над множествами

функция вида 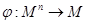называется n-арной операцией на множестве М

операция 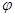ассоциативна.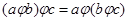

операция 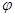коммутативна.

так же существуют свойство, верные не для всех операций.

операция 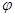называется дистрибитивно слева относительно операции если

операция 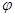называется дистрибитивно справа относительно операции если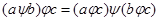

Отображения множеств

понятие отоброжения множеств неразрывно связано с понятием функции. Функцией называют функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то 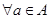соответствует единственное 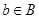(более привычная форма - f(a)=b). обозначается как

Полностью заданная функция называется отображением множества А на множество В.

Дата добавления: 2015-09-06