Определение параметров, характеризующих колебательный процесс кузова

Параметрами, характеризующими колебания кузова вагона-цистерны на пружинах рессорного подвешивания, являются амплитуда А, период колебаний Т и частота колебаний ν.

Значения периода и амплитуды колебаний возьмем с графиков, приведенных на рисунках 5 – 10. Определенные по графикам параметры А и Т и рассчитанные значения ν приведены в таблице 3.

Формула для определения частоты колебаний ν, Гц, имеет вид (25):

, (25)

где Т – период колебаний, с.

Т₁ = 0,61 – 0,29 = 0,32 (с);

Т₂ = 0,575 – 0,27 = 0,305 (с);

Т₃ = 0,56 – 0,27 = 0,29 (с);

Т₄ = 0,535 – 0,26 = 0,275 (с);

Т₅ = 0,515 – 0,245 = 0,27 (с);

А₁ = 0,028 - 0,0279 = 0,0001 (м);

А₂ = 0,025 - 0,02524 = -0,00024 (м);

А₃ = 0,023 - 0,02349 = -0,00049 (м);

А₄ =0,021 - 0,02169 = -0,00069 (м);

А₅ = 0,02 - 0,02071 = -0,00071 (м);

Таблица 3 – Параметры собственных колебаний кузова цистерны 15-1482

Жесткость рессорного подвешивания С, Н/м	Параметры колебаний
Амплитуда А, м	Период Т, с	Частота n, Гц
	0,0001	0,32	3,125
	0,00024	0,305	3,278
	0,00049	0,29	3,448
	0,00069	0,275	3,636
	0,00071	0,27	3,704

Рассчитаем погрешности амплитуды и частоты для каждой жесткости по формулам (26) и (27):

, (26)

, (27)

%;

%;

%;

%;

%;

%;

%;

%;

%;

%;

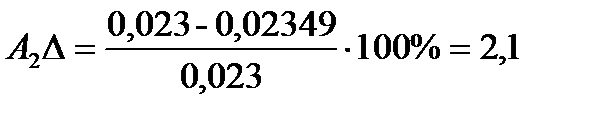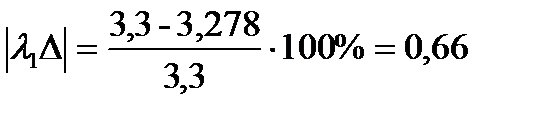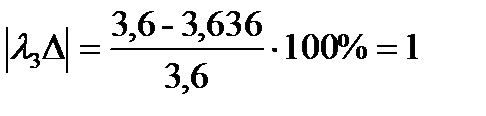Подсчитали погрешность каждой амплитуды и частоты колебаний при различной жесткости рессорного подвешивания. Полученная погрешность не превышает допустимой, которая равна 15%. Следовательно, можно сделать вывод, что математическая модель и алгоритм решения задачи разработаны верно.

Дата добавления: 2015-09-06