Вывод уравнений математической модели

Математическая модель в динамике твердых тел представляет собой систему, в которую входят начальные условия и уравнение движения. Для получения уравнения движения математической модели воспользуемся принципом Д’ Аламбера. Сущность выше указанного принципа заключается в следующем:

- непрерывный процесс колебаний делим на равные временые интервалы и рассматриваем поведение системы именно в этих точках;

- поскольку тело находится в движении всегда присутствует сила инерции, приложенная к центру масс;

- для каждого временного интервала составляем уравнение равновесия.

Согласно вышеуказанному принципу, вырезаем твердое тело, в данном случае это будет котел цистерны, реакциями упругих элементов будет действие отброшенных связей, приложим к твердому телу все внешние силы и силы инерции в центре масс. Сила инерции направлена в сторону, противоположную направлению движения q. Основная система изображена на рисунке 3 [8].

Рисунок 3 – Основная система

где q – обобщенная координата. Физический смысл обобщенной координаты заключается в перемещение центра тяжести при колебаниях;

R – реакция упругих элементов.

Для записи уравнения равновесия введем ось движения , , . Спроецируем все силы, действующие на кузов, на ось движения, и получим уравнение движения (9):

, (9)

где – ускорение перемещения кузова;

R – реакция рессорного подвешивания;

M – масса кузова.

Ноль в правой части уравнения говорит о том, что колебания являются собственными (свободными), что соответствует условию задачи. Полученные уравнения движения имеют две вариативных формы записи (10):

(10)

Для нахождения начальных условий воспользуемся первой формой записи уравнения из формулы (10). Поскольку после установки груза в кузов тело находится в состоянии покоя (отсутствуют перемещения), то , = 0, тогда получим (11), (12):

(11)

(12)

Итак получили математическую модель собственных колебаний кузова на рессорном подвешивании, которая включает в себя уравнение движения и начальные условия (13):

(13)

Определим начальное перемещение при максимальной и минимальной жесткости рессорного подвешивания из уравнения (12). Так как по заданию дано с для одной пружины, в одном рессорном комплекте их 5 то уравнение (12) поучим в следующем виде

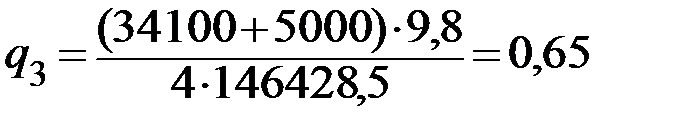
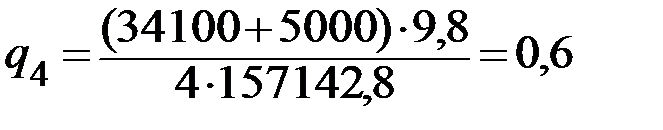
(9)

Дата добавления: 2015-09-06