Анализ диапазона частот и амплитуд собственных колебаний объекта исследования

На колебательный процесс кузова вагона влияют следующие параметры: жесткость рессорного подвешивания, масса кузова, масса груза, база вагона.

При увеличении массы кузова вагона частота колебаний уменьшиться, но амплитуда колебаний увеличится и наоборот – уменьшение массы ведет к увеличению частоты колебаний и уменьшению амплитуды колебаний.

Масса груза это необходимый параметр для определения начальных условий колебательного процесса.

Жесткость рессорного подвешивания – это главный параметр, влияющий на колебательный процесс кузова вагона. При прохождении колесными парами какой-нибудь неровности пути возникают динамические нагрузки, в том числе и удары, при этом колесные пары и буксы испытывают весьма большие ускорения.

При отсутствии рессорного подвешивания кузов жестко воспринимает все динамические воздействия. При высокой жесткости рессорного подвешивания амплитуда колебаний уменьшается, удары воспринимаемые колесными парами не гасятся, частота колебаний увеличивается. При слишком малой жесткости рессорного подвешивания амплитуда увеличивается, что нежелательно.

Приближенное значение частоты колебаний вагона определяют по формуле 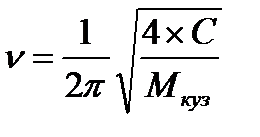1:

(1)

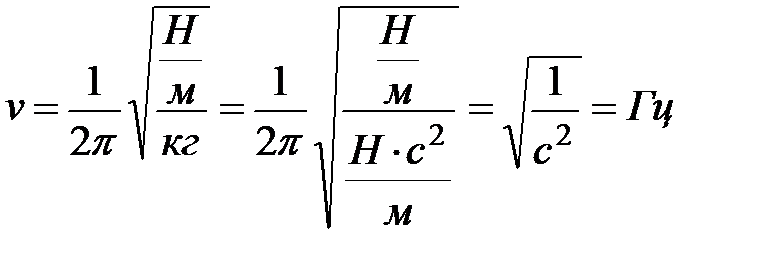
где С – жесткость рессорного подвешивания, Н/м;

М – масса кузова вагона, т.

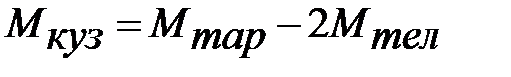(2)

где – масса кузова;

– масса тары;

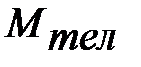– масса тележки 68-875.

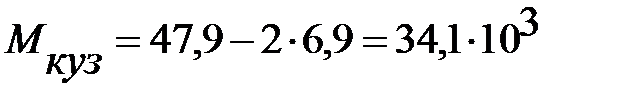кг.

Тележка модели 68 – 875 имеет коэффициент вертикальной динамики k_дв, вычисляемый по формуле (3) [4]:

(3)

где 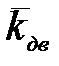– среднее вероятное значение коэффициента вертикальной динамики;

β – параметр распределения (уточняется по экспериментальным данным), для пассажирских вагонов при существующих условиях эксплуатации β=1;

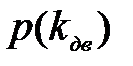– вероятное распределение, согласно расчетным режимам 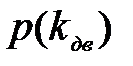=0,97.

При скоростях движения вагона υ≥15 м/с, 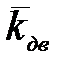рассчитывается по формуле 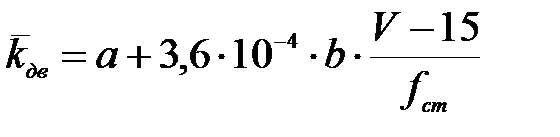(4):

(4)

где а – коэффициент, принимаемый на основании обработки результатов теоретических и экспериментальных исследований равная для обрессоренных частей тележки – 0,1;

V – расчетная скорость движения вагона, м/с, (V =44,4 м/с);

f _{с т} – статический прогиб рессорного подвешивания, м, (f _{с т} =0,221 м);

b – коэффициент учитывающий влияние числа осей в группе тележек (n=2) под одним концом вагона на величину коэффициента динамики (формула (5)):

(5)

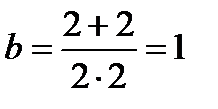
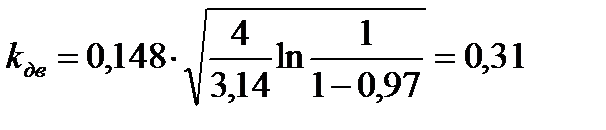
Тогда амплитуду A, равную полному статическому прогибу f _полн.max, находим по формуле (6):

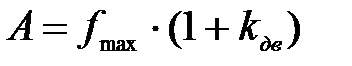(6)

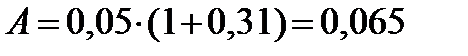(м).

Жесткость рессорного подвешивания тележки ТВЗ-ЦНИИ:

С=1/λ,

где λ-гибкость рессорного подвешивания тележкт ТВЗ-ЦНИИ по ТЭП (4,98-8,97) взяли среднее λ=7 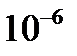м/кг

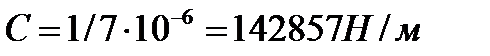(3)

Следовательно, минимальное и максимальное значения жесткости будут равны:

C_min=C – C∙0,2 = 142857 – 28571,4 = 114285,6 Н/м;

C_max=C + C∙0,1 = 142857 + 14285,7 = 157142,7 Н/м;

Мы получили диапазон жесткостей (114285,6; 157142,7);

157142,7 – 114285,6 =42857,1

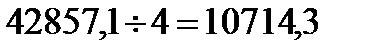
Отсюда получаем новые величины жесткости:

С₀= 114285,6 Н/м;

С₁ = 114285,6 + 10714,3 = 124999,9 Н/м;

С₂ = 124999,9 +10714,3 = 135714,2 Н/м;

С₃ = 135714,2 +10714,3 = 146428,5 Н/м;

С₄ = 146428,5 +10714,3 = 157142,8 Н/м.

Вычислим частоты колебаний кузова в порожнем состоянии.

при С₀=114285,6 Н/м, М_куз=34.1т =34100 кг:

при С₁= 124999,9 Н/м, М_куз = 34,1т =34100 кг:

при С₂= 135714,2 Н/м, М_куз = 34,1т =34100 кг:

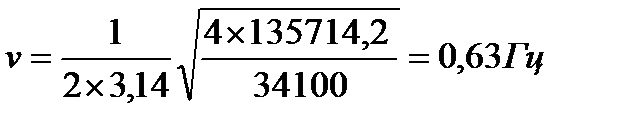
при С₃= 146428,5 Н/м, М_куз = 34,1т =34100 кг:

при С₄= 157142,8 Н/м, М_куз = 34,1 =34100 кг:

Вычислим частоту колебаний кузова при груженом состоянии по формуле 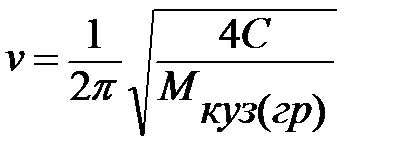(4)

(4)

где 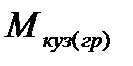- масса груза плюс масса кузова вагона;

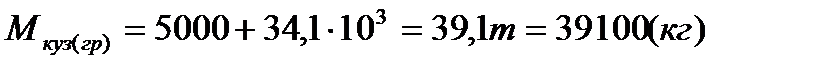
При С =114285,6 Н/м, 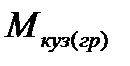=39100 кг:

;

При С =157142,8 Н/м:

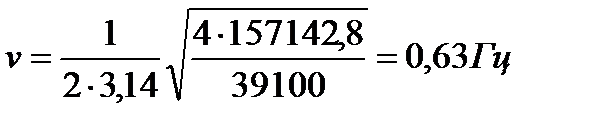
Для двухосного пассажирского вагона модели 61 - 836 получили диапазон частот колебаний в порожнем состоянии вагона 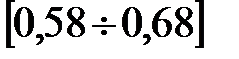Гц, а при груженом состоянии 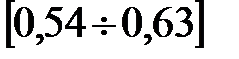Гц.

---

Дата добавления: 2015-09-06