Описание алгоритма выбранного метода решения обыкновенных дифференциальных уравнений

Для интегрирования полученного обыкновенного дифференциального уравнения колебания кузова вагона на рессорах был выбран разностный метод интегрирования.

Обратимся к математической модели собственных колебаний подпрыгивания кузова вагона на пружинах рессорного подвешивания система уравнений (9)

(10)

В математической модели выражение для массы М может принимать 2 значения система (11)

(11)

Первое значение в выражении (11) для массы М соответствует состоянию статического равновесия вагона с грузом в момент времени t = 0. Второе значение в выражении (11) для массы М соответствует колебательному процессу после снятия нагрузки массой Мг.

Алгоритм решения этим методом заключается в следующем:

- Определяем наивысшую производную степень ОДУ.

- Дифференциальное уравнение первого порядка заменяем разностным аналогом (формула 11)

. (11)

где – перемещение при текущем (i) значении времени;

– перемещение при предыдущем (i-1) значении времени;

h – шаг интегрирования (шаг разностной аппроксимации по времени).

- Производная второго порядка заменяется разностным аналогом (формула 12)

(12)

где 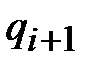– перемещение при последующем (i+1) значении времени;

– перемещение при текущем значении времени;

– перемещение при предыдущем значении времени;

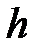– шаг интегрирования по времени.

- Разностные аналоги подставляются в исходное уравнение.

- Определяем начальные условия.

Подставляем:

(13)

(14)

(15)

Уравнение (14) является алгебраическим аналогом дифференциального уравнения движения в системе (8). Математическая модель собственных колебаний подпрыгивания в разностной форме примет вид

(16)

Дата добавления: 2015-09-06