Классический образец современной астрономии

Есть здесь смысл обогатиться и вторым вариантом научного академического знания, чтобы внимательнее рассмотреть две точки зрения и принять уже собственный соответствующий вывод, а не блуждать в поисках истины очередного гипнотизера около выдвинутой неудачной научной версии.

Нас заставляли раньше, да и до настоящего момента заставляют думать, как в церкви – по вере, без права на собственное решение иной задачи и возможности её дальнейшего утверждения.

Хоть раз вдумайтесь: каким образом «древний» Аристотель мог измыслить «сферы хрустальных небес», минуя церковную аксиому «тверди небесной». В этом случае можно лишь дополнить, что кроме познания научной точности «Аристотель» ещё обладал и даром предвидения, о котором не было отражено в позднейших его исторических трудах.

Но если чуть-чуть изменить положение предоставленной истины и поставить, предполагая, труды «древнего Аристотеля» после утверждённого церковного догмата о «тверди небесной», то всё станет на свои места. И будет выяснено, что «древняя» научная мысль оттолкнулась впервые только от однажды брошенной фразы, что над головой существовала «твердь небесная». Впоследствии и до настоящего дня естественные науки стали изучаться именно по этому, ошибочно выбранному, курсу знаний. Такова сила волшебного змеиного взгляда традиции, а не гибкого научного решения, могущего в корне изменить форму прежнего познания современными и более совершенными методиками.

Итак, внимательно вспоминаем школьный курс астрономической науки:

«Прежде всего напомним, что при изучении вида звёздного неба пользуются понятием небесной сферы – воображаемой сферы произвольного радиуса, к внутренней поверхности которой как бы «подвешены» звезды. В центре этой сферы (в точке 0) и находится наблюдатель (рис. 1). Точка небесной сферы, расположенная прямо над головой наблюдателя, называется зенитом, противоположная ей – надиром. Точки пересечения воображаемой оси вращения Земли («оси мира») с небесной сферой называются полюсами мира.

Проведем через центр небесной сферы три воображаемые плоскости: первую перпендикулярно к отвесной линии, вторую перпендикулярно к оси мира и третью – через отвесную линию (через центр сферы и зенит) и ось мира (через полюс мира). В результате на небесной сфере получим три больших круга (центры которых совпадают с центром небесной сферы): горизонт, небесный экватор и небесный меридиан (рис. 1). Небесный меридиан пересекается с горизонтом в двух точках: точке севера (N) и точка юга (S), небесный экватор – в точке востока (E) и точке запада (W). Линия SN, определяющая направление «север – юг», называется полуденной линией.

Видимое годичное передвижение центра диска Солнца среди звезд происходит по эклиптике – большому кругу, плоскость которого составляет с плоскостью небесного экватора угол e =23 градуса 27 минут. С небесным экватором эклиптика пересекается в двух точках (рис. 2): в точке весеннего равноденствия и в точке осеннего равноденствия.

Напомним, что Солнце передвигается по эклиптике навстречу видимому суточному вращению небесной сферы (т.е. с запада на восток) со скоростью почти 1 градуса в сутки, что составляет два его видимых угловых диаметра. Через точку весеннего равноденствия Солнце проходит 20 (или 21) марта, двигаясь из южного полушария в северное. Полгода спустя 22 (или 23) сентября оно проходит через точку осеннего равноденствия из северного полушария в южное.

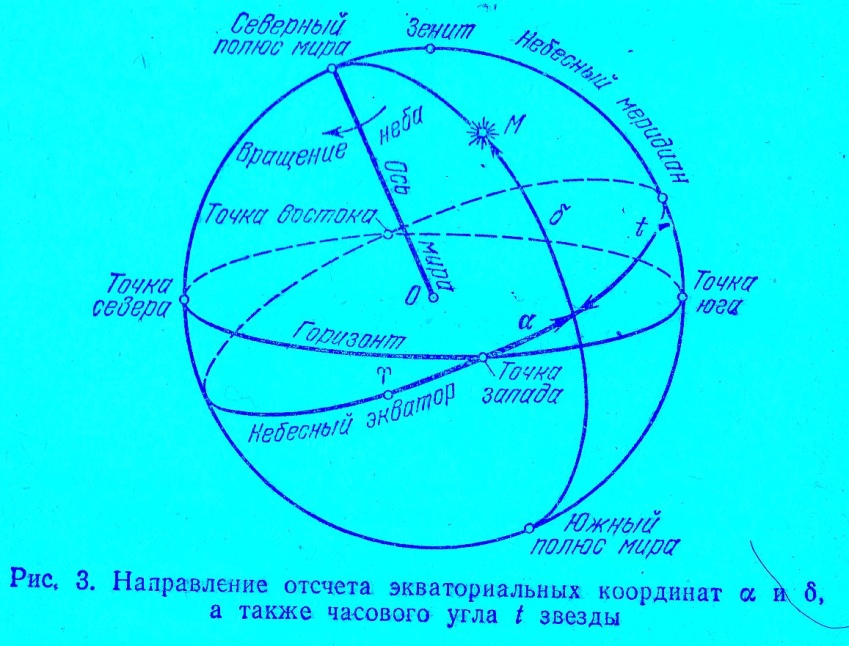
Как и на глобусе – уменьшенной модели Земли, на небесной сфере (но изнутри нее!) можно построить координатную сетку, позволяющую определить координаты любого светила. Роль земных меридианов на небесной сфере играют круги склонений, проходящие от северного полюса мира к южному, вместо земных параллелей на небесной сфере находятся суточные параллели. Для каждого светила можно найти направление отсчета экваториальных координат a и б, а также часового угла t звезды (рис. 3).

Угловое расстояние а его круга склонения от точки весеннего равноденствия, измеренное вдоль небесного экватора против суточного движения небесной сферы (аналогично тому, как вдоль земного экватора мы измеряем географическую долготу – угловое расстояние меридиана наблюдателя от нулевого гринвичского меридиана). Эта координата называется прямым восхождением светила.

Дата добавления: 2015-10-13