Разность матриц A и B будем обозначать A-B.

Произведением матрицы на число называется матрица , элементы которой определены равенством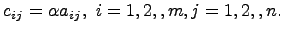

Произведение матрицы A на число будем обозначать .

Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами:

1) ;

2) ;

3) (Распределительное свойство относительно сложения матриц);

4) (Распределительное свойство относительно сложения чисел);

5) -A=(-1)A.

Все перечисленные свойства непосредственно вытекают из определения.

Операции сложения матриц и умножения матрицы на число позволяют для произвольных матриц одинакового размера 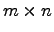и произвольных чисел однозначно определить матрицу , называемую линейной комбинацией матриц с коэффициентами .

Умножение матриц. Произведением матриц и называется матрица , элементы которой определены равенством

Произведение матриц A и B будем обозначать C=AB.

Из определения следует, что произведение AB определено лишь в том случае, когда число столбцов матрицы A совпадает с числом строк матрицы B. Это означает, что оба произведения AB и BA определены тогда и только тогда, когда матрицы A и B имеют размеры 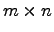и соответственно. Следовательно равенство AB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.

Матрицы A и B называются перестановочными или коммутирующими, если AB=BA.

Теорема 2.3 Операция умножения матриц обладает следующими свойствами:

1) (AB)C=A(BC); (Свойство ассоциативности)

2) , для любого действительного числа

3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C, для которых левые части равенств имеют смысл.

Справедливость свойств 2) и 3) доказываются непосредственно.

В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть , , 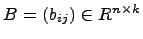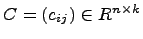. Матрицы A(B+C) и AB+AC имеют одинаковый размер - . Пусть - элемент матрицы A(B+C) в позиции (i,j), 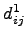- элемент матрицы AB+AC в позиции (i,j), тогда

Из равенств (1) и (2) следует, что , что доказывает первое равенство свойства 3).

Подробное доказательство свойства 1) можно найти в учебнике В. А. Ильин, Г. Д. Ким "Линейная алгебра и аналитическая геометрия".

Заметим, что для любой матрицы и единичных матрицы и справедливо:

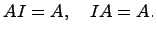
Транспонирование матриц. Пусть . Матрица называется транспонированной к матрице A, если

Транспонированная матрица также обозначается символами и .

Заметим, что при транспонировании матрицы её строки становятся столбцами матрицы , с теми же номерами, а столбцы - строками.

Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами:

1) ;

2) , для любого действительного числа ;

3) ;

4) , для любых матриц A и B, для которых имеют смысл левые части равенств.

Свойства 1), 2), 4) непосредственно вытекают из определения.

Приведём доказательство свойства 3). Пусть и 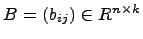, при таком согласовании размеров матриц A и B произведения AB и существуют, при этом размеры и совпадают и равны . Пусть - элемент матрицы AB в позиции (i,j), - элемент матрицы , - элемент матрицы в позиции (i,j).

что доказывает справедливость свойства 3).

Дата добавления: 2015-08-21