Свойства смешанного произведения

1. Смешанное произведение не меняется при циклической перестановке его сомножителей (не меняется ни объем параллелепипеда, ни ориентация его ребер): .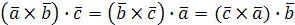

2. Смешанное произведение не меняется 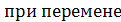знаков векторного и скалярного умножения: 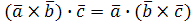, поэтому смешанное произведение записывают .

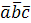3. Смешанное произведение меняет свой знак при перемене любых двух вектор-сомножителей: , .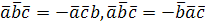

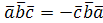4. Смешанное произведение ненулевых векторов 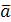, 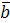и 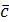равно нулю тогда и только тогда, когда они компланарны: 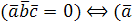, , 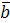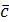– компланарны .

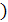Доказательство. Предположим, что векторы 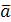, 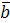и 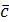– не компланарны. Тогда можно построить параллелепипед имеющий объем 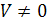, т.е. 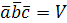, но это противоречит условию, согласно которого, 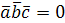. Следовательно, векторы 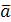, 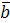и 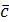– компланарны.

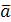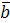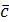Обратно, пусть , и – компланарны. Тогда вектор 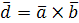и перпендикулярен плоскости, в которой находятся векторы 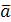, 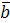и 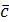, значит, он перпендикулярен любому вектору, лежащему в этой плоскости, например 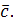Это значит, что .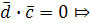

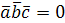Смешанное произведение векторов, заданных своими проекциями в декартовой системе координат.

Пусть векторы заданы своими разложениями по ортам в декартовой системе координат:

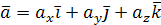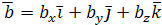, и .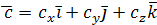

Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

.

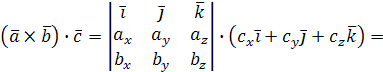
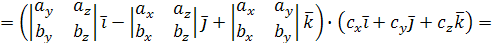
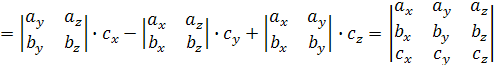Итак,

.

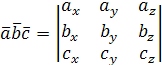Дата добавления: 2015-08-21