Матрицы: определения, операции над матрицами

Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

(4.1)

или сокращенно в виде A = (a _{i j}) (i = ; j = ). Числа a _{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a _{i j}) и B = (b _{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a _{i j} = b _{i j}.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

Если все элементы a _{i i} диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

.

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Равенство матриц. Две матрицы и 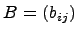одинакового размера m на n называются равными, если , i = 1,2,…,m, j=1,2,…,n.

Если матрицы A и B равны, то будем писать A=B.

Линейные операции. Суммой двух матриц A и B размера m на n называется матрица C размера m на n, элементы которой определяются равенством

Сумму матриц A и B будем обозначать C=A+B.

Матрица 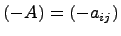называется противоположной к матрице .

Теорема 2.1 Операция сложения матриц обладает следующими свойствами: для любых матриц и нулевой матрицы

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.

Разностью матриц и называется матрица A+(-B).

Дата добавления: 2015-08-21