Ағымдар, инциденциялар және аралас матрицаларды анықтау.

Ағымдардың матрицасы – ол әрбір қатардағы үш бүтін сандардың тізбегі: бірінші сан – ағым нөмірі, екіншісі – ақпарат шығатын аппарат нөмірі. Қоректенетін ағымдар №0-ші блоктан келетін деп, ал өнім ағымы №0-ші блокқа келетін деп көрсетілді. Ағымдар матрицасында есептегі блоктың типін (түрін) және блок ағымдарының кіру және шығу реттілігін көрсететін көрсетулер болмайды.

Инциденциялар матрицасының сол бағанасында аппарат нөмірі, ал қалған бағаналарында ағымдардың нөмірлері болады. +1 осы бағанада нөмірі берілген ағымның нөмірі қатарда берілген аппаратқа кіретінін (енетінін), ал –-1 ағымның аппараттан шығатынын көрсетеді. Егер бағаналардың қосындысы 0-ге тең болса, онда ағым екі блокпен байланысқан болады. Егер олардың қосындысы +1-ге тең болса, онда блок қороектенегін блок, ал қосынды –1-ге тең болса, ол өнімнің ағымы болады. Процесте рециркулияциялық ағымның болуы инциденциялық матрицасы бойынша анықталады. Егер қатарларды ауыстырғанда әрбір бағнада +1-ден –1 аспаса, қосындысы 0 болады.

Аралас матрица – ол қатарлардың нөмірі мен бағаналардың нөмірі белгілі бір блокқа сәйкес келетін квадраттық матрица. “1” қатар нөмірі берілген блок пен бағана нөмірі берілген блоктың байланысын көрсетеді. “0” олардың арасында байланыстың жоқ екені көрсетеді. Аралас матрица рециклдерді табуда пайдалы, бірақ онда ақпараттардың көлемі аз болады, яғни онда қоректенетін ағымдар, өнімдер ағымдары және ағымдардың нөмірлері көрсетілмеген.

Тұйықтылығы үзілген тұйық сұлбалар, рециркуляциялық тізбектіліктер. Тұйықтылығы үзілген сұлба – ол рециклі жоқ сұлба. Рециклі жоқ процестің бөлігін тізбектілігі (тұйықтыға) үзілген деп атайды. Мұндай сұлбаның блоктарын кіретін белгілі қоректенетін ағымдары бар блоктан бастап, біртіндеп бірінен кейін бірін есептейді. Бұл блоктың шығулары келесі блокқа енетін белгілі енулер болып табылады.

Тұйық сұлбалар – блоктан шығатын ағым оған кіретін ағымдардың кем дегенде біреуіне әсер ететін сұлбалар. Сұлбаның тұйық бөлігінен ағымдар келетін сұлбаның тұйықтығы үзілген бөлігі де болуы мүмкін. Бір-бірімен тізбектеліп байланысқан түйық сұлбалар рециркуляциялық тізбектілік деп аталады. Бұл жағдайда процесті есептеу жоспары мыналардан тұрады:

1) Тұйықтылы үзілген және рециркуляциялық тізбектіліктерді және олардың есептеуге лайықты мүмкіндіктегі тізбектілікте орналасуын анықтау.

2) Әрбір рециркулияциялық тізбектілікті есептеу әдісін табу.

Аралас матрица дәрежесін анықтау жолымен рециркуляциялық тізбектілерді анықтау.

Нөлдік қатарлар мен бағаналарды жойғаннан кейін алынған қысқартылған аралас матрицаны А рециркуляциялық тізбектілерді, сондай-ақ әрбір тізбектіліктегі контурларды идентификациялау үшін пайдаланады. Бұл әдіс аралас матрицаларды көбейту жолымен аралас матрица дәрежесін анықтауға негізделген. Екі А және В матрицаның көбейтіндісінің элементі (i,j) 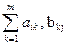болады, мұндағы 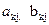А және В матрицаларына сәйкес 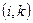-элементтері. Бірақ бұл жағдайда Бульев арифметикасы болады, яғни:

Бульев қосындысы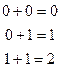

Бульев көбейтіндісі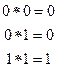

яғни, ол барлық оң бүтін сандарды – мен ауыстырғандағы кәдімгі арифметикаға эквивалентті болады.

А-ны өзіне өзін тізбектеп көбейтіп А-матрицасының n-дік дәрежесі алынғанда, Аⁿ кез-келген блоктың кез-келген блокқа "n" ағымдары арқылы өтетін байланыстарды көрсетеді. Егер матрица үшін a_ij=1 болса, Аⁿ "n" ағымдары арқылы қатарына сәйкес і – блогінен j –бағанасына сәйкеес блокқа өтетін ең болмағанда бір жол бар болатынын көрсетеді. Егер a_ij=0 болса, онда ондай байланыс жоқ болғаны.

Егер Aⁿ(n=2,3,…) тұйық сұлба тұйық сұлба үшін алынған болса, онда оның кейбір диагнольдік элементтері ең ақырында бірліктерге айналады. Алайда, диагнольдік бірлікке сәйкес келетін кезкелі і-ші блок "n" ағымдарының і блогіндегі өздерінің байланысы болады, яғни контур алынады. Б қондырғысы үшін А матрицасының дәрежелері кестеде беріледі.

Блоктардың рецеркуляциялық тізбектілерін идентификациялау – жетісушілік матрицасы.

Егер А матрицасының дәрежелерінің Бульевтік қосындысы түзілсе, онда матрица дәрежесінің қандай да бір элементіне сәйкес тек бір ғана элементі бірге (1) тең болса, онда оның элементі 1-ге тең болады.

Шешуші матрицада 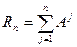(1) саны 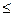n ағымдары арқылыы і -блогінен j -блогіне өтетін байланыстар болады. Сонда R_n матрицасының r_ij элементі егер ең кем дегенде осындай бір байланыс болғанда ғана 1-ге тең болады. n→∞, R_n→R_∞ шегінде жетістік матрицасы і -блогінен j-блогіне ағымдардың кез-келген (шектік) саны арқылы өтетін қандай да бір байланыс бар жоқтығын жазады. Сонымен, егер і- j –дің қандай да бір байланысы болғанда ғана 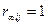болады екен.

А немесе R_m-ді тасымалдайық, яғни А^Т немесе 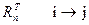барлық байланыстарының бағыттарын өзгертеді, өйткені қатарлар бағаналарға айналады және керісінше болады. Рециркуляциялық тізбектілікте тек ғана i→j байланыстары емес, сонымен қатар оның тасымалданған түрімен 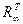жанасса, онда бірлік 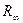және 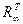- да болған жерлерде ғана сақталады. Қилысу нәтижесі былай жазылады:

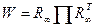(2)

Енді егер блок-сұлбада i→j байланысы болғанда ғана 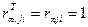болады. Ендеше тек егер 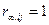және 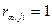, яғни і↔j,болғанда ғана 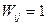болады. Бұл рециркуляциялыық тізбектілердің ең болмағанда біреуіне кірмейтін блокты шығарады (кетіреді), өйткені ол блоктан екі бағыттағы да ешқандай кез-келген блокқа байланыс болмайды. Блоктардан рециркуляциялық тізбектілігінің анықтамасы бойынша оны барлық мүшелері өзара байланысты. Рециркуляциялық тізбектілікке кірмеген және W-да нольдік емес қатары бар кезкелген блок блоктардың рециркуляциялық тізбектілігінің бар екенін көрсетеді. Рециркуляциялық тізбектілердің біреуіне кірмейтін және кіретін, иә шығатын емес кезкелген блок екі рециркуляциялық тізбектілердің арасындағы блоктардың тұйықтағы үзілген тізбектілігіне кіреді. Оны оның алдындағы рециркуляциялық тізбектілік есептелгеннен соң есептейді.

Рециркуляциялық тізбектілікті идентификацияла- ғаннан кейін оны есептеу мәселесі тұрады. Оны шешудің 2 әдісі бар:

1. Тізбектеп есептеу, яғни бір блокты басқадан кейін бір итерациядағы кез-келген айнымалы ағымдағы өзгеріс бұрынғы бекітілген рұқсат етілген ауытқудан аз болғанға дейін қайталап есептеу.

2. Бірденнен есептеу, яғни тізбектіліктің барлық блоктары бірденнен сандық әдістермен шешіледі. Әдетте процестер бейсызықты болғандықтан итерацияны өндіру қажет болады. [5].

Дата добавления: 2015-09-03