
Читайте также:
|
Тема урока: Обыкновенные дроби.
Цель: способствовать повышению интереса к предмету.
Задачи: в игровой форме обобщить и систематизировать знания и умения учащихся по теме урока; воспитывать стремление к активному участию в работе на уроке; воспитывать у учащихся умение совместно работать в коллективе, умение объективно оценить свой труд и труд одноклассников; развивать память, внимание, умение говорить.
Ход урока:
I. Организационный момент (5 мин.)
1. Цель урока.
2. Правила игры.
II. Игра (32 мин.)
1. Викторина (теоретический конкурс) (5 мин.)
(За каждый правильный ответ команда получает 1 балл).
1) Дайте понятие обыкновенной дроби.
2) Что показывает знаменатель обыкновенной дроби?
3) Что показывает числитель обыкновенной дроби?
4) Какая дробь называется правильной? Приведите примеры.
5) Какая дробь называется неправильной? Приведите примеры.
6) Как сравнить дроби с одинаковыми знаменателями?
7) Можно ли сравнить две дроби с разными знаменателями и разными числителями, если известно, что одна дробь правильная, а другая – неправильная?
8) Как складывают дроби с одинаковыми знаменателями?
9) Как вычитают дроби с одинаковыми знаменателями?
10) Дайте понятие смешанного числа.
2. Вперед, вперед, вперед (устная работа в форме диктанта) (7 мин.)
Выполняют все учащиеся (каждый в своей тетради).
Вычислите:
1)  2)
2)  3)
3)  4)
4) 
| Сравните:
1)  2)
2)  3)
3) 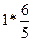 4)
4) 
| Впишите в рамочку нужное число:
1)  = 1
2) - 1 = = 1
2) - 1 = 
|
После 4 мин. работы каждый должен сам оценить себя, сравнив свои ответы с правильными.
Оценка «5» - 10 правильных ответов
«4» - 8-9 правильных ответов
«3» - 5-7 правильных ответов
«см» - 4 и меньше правильных ответов
Оценку команде ставит капитан, оценив результаты своей команды.
3. Конкурс команд (13 мин.)
Каждой команде выдаются по три карточки с заданиями (у команд карточки одинаковые). Время ограничено (8 мин.), решить задания кто-то один не успеет, поэтому задания должны быть разделены между учащимися и проверены.
Карточка №1.
Найдите ошибки (если ответ неверный, зачеркните его и напишите верный):
1)  2)
2)  3)
3)  4)
4) 
| Карточка №2.
Определите правило нахождения числа, стоящего посередине, по этому же принципу вставьте пропущенное число:
1)  ; ; 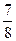 ; ; 
 ;?; ;?;  2)
2)  ; ;  ; ; 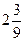
 ;?; ;?;  3)
3)  ; ;  ; ; 
 ;?; ;?; 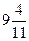
| Карточка №3.
Решите уравнения:
1)  2)
2) 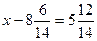 3)
3) 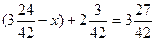 4)
4) 
|
Когда время закончится, карточки с ответами сдаются членам жюри, у доски проверяются и анализируются ответы.
(За каждый правильный ответ команда получает 1 балл).
4. Тест (7 мин.)
Каждому ученику выдается карточка с тестом, на которой он отмечает вариант ответа.
Тест №1, №3, №5, …
1) Даны дроби: 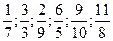 .
Какие из них являются правильными?
А) .
Какие из них являются правильными?
А) 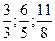 Б) Б)  В) В)  2) Какое число стоит между числами
2) Какое число стоит между числами
 и 1?
А) и 1?
А)  Б) Б)  В) В)  Г) Г) 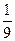 3) Представьте неправильную дробь
3) Представьте неправильную дробь  в виде смешанного числа.
А) в виде смешанного числа.
А)  Б) Б) 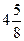 В) В) 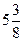 4) Представьте смешанное число
4) Представьте смешанное число  в виде неправильной дроби.
А)
в виде неправильной дроби.
А)  Б) Б)  В) В)  5) Вычислите
5) Вычислите  А)
А)  Б) Б)  В) В)  6) Вычислите
6) Вычислите 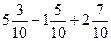 А)
А)  Б) Б)  В) В)  7) Вычислите число, которое должно стоять в квадрате 2 - - 1 =
7) Вычислите число, которое должно стоять в квадрате 2 - - 1 = 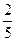 .
А) .
А)  Б) Б) 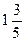 В) В) 
| Тест №2, №4, №6, …
1) Даны дроби: 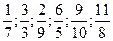 .
Какие из них являются неправильными?
А) .
Какие из них являются неправильными?
А) 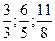 Б) Б)  В) В)  2) Какое число стоит между числами
2) Какое число стоит между числами
 и 1?
А) и 1?
А)  Б) Б)  В) В)  Г) Г)  3) Представьте неправильную дробь
3) Представьте неправильную дробь 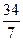 в виде смешанного числа.
А) в виде смешанного числа.
А)  Б) Б)  В) В)  4) Представьте смешанное число
4) Представьте смешанное число 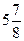 в виде неправильной дроби.
А)
в виде неправильной дроби.
А)  Б) Б)  В) В)  5) Вычислите
5) Вычислите 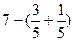 А)
А) 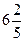 Б) Б)  В) В)  6) Вычислите
6) Вычислите  А)
А)  Б) Б)  В) В)  7) Вычислите число, которое должно стоять в квадрате 2 - - 1 =
7) Вычислите число, которое должно стоять в квадрате 2 - - 1 =  .
А) .
А)  Б) Б) 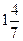 В) В) 
|
По истечении 5 мин. карточки с вариантами ответов для проверки передаются команде соперников.
Учитель на доске открывает ответы к тестам:
Тест №1, №3, №5, …: 1) В; 2) Б; 3) Б; 4) А; 5) Б; 6) А; 7) В.
Тест №2, №4, №6, …: 1) А; 2) В; 3) А; 4) В; 5) Б; 6) Б; 7) А.
Оценка «5» - 7 правильных ответов
«4» - 5-6 правильных ответов
«3» - 4 правильных ответа
«см» - 3 и меньше правильных ответов
III. Итоги урока (3 мин.)
1. Учитель просит оценить себя и свою группу, в тетради поставить оценку
себе и своей группе и сдать тетради на проверку.
2. Учитель объявляет число баллов, набранных командами (по итогам конкурсов).
3. Учитель благодарит всех за урок.
Дата добавления: 2015-08-21; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формы контроля | | | Технология проблемного обучения |