Спосіб 1. Розглянемо множину SС(2n), отриману на n-ому кроці побудови килима Серпінського SС(2).

Лема 1. Нехай х₀= , у₀₌ , .

M(x₀,y₀) SC⁽²⁾

Доведення леми проведемо методом математичної індукції:

1 крок: n= 1

М(x₀,y₀)

Рис. 3.16.

М(х_0, у₀) DАВЕÛ

М(х₀,у₀)ÎDCEFÛ

У загальному випадку точка

М(х₀,у₀)ÎSC₁⁽²⁾

Отже, твердження справедливе для п = 1.

2 крок: припустимо, що твердження виконується для n = k, тобто

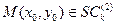
і доведемо виконується для п = k + 1, тобто

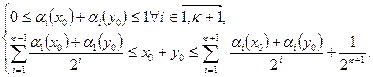
Нехай точка М(х₀,у₀) на k- омукроці попала в один з 3^k трикутників, її координати записуються у вигляді

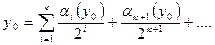
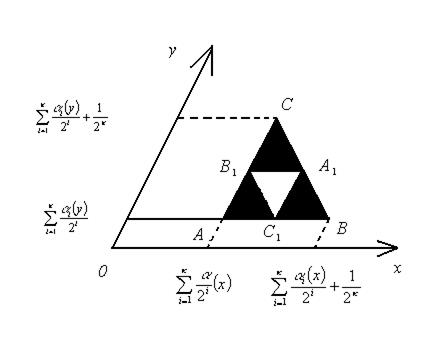
Рис. 3.17.

Розглянемо трикутник АС₁В₁. Його точки задовольняють таким умовам: всі вони лежать нижче прямої В₁С₁ та

Запишемо рівняння прямої В₁С₁:

В₁С₁: х + у =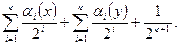

Тоді точка М(х₀ ,у₀)Î

Аналогічно, розглядаючи трикутники С₁ВА₁ та В₁А₁С маємо:

М(х_0,у₀)ÎDС₁ВА₁Û

М(х₀,у₀)ÎDВ₁А₁СÛ

Врахувавши значення a_k+1(х₀) та a_k+1(у₀) у кожному з трикутників, у загальному випадку можемо записати, що точка

М(х_0,у₀)ÎSC_k+1⁽²⁾Û

3 крок. Тому, за аксіомою індукції твердження правильне при кожному натуральному п. Лему доведено. [Посилання на Твердохлібову]

Теорема 3.1. Нехай х = тоді

М(х,у)ÎSC⁽²⁾ Û 0 a_і(х)+a_і(у) 1 .

Доведення. Трикутний килим Серпінського SC⁽²⁾ є перерізом усіх множин, які утворюються на першому, другому,..., -ому,... кроці побудови, тобто

SC⁽²⁾= = SC⁽²⁾_n.

Розглянемо множину SС⁽²_n⁾, яку отримали на -ому кроці побудови трикутного килима Серпінського, За щойно доведеною лемою 1

M(x,y) SC_n^{(2 )}

В останній системі зробимо граничний перехід, при п

М(х,y) SС⁽²⁾ Û

Користуючись тим, що х= маємо:

Û 0 . Доведено.

Отже, розглядали одиничний паралелограм, кожна сторона якого поділена навпіл. Тоді сам паралелограм поділяється прямими на 4 менші паралелограми. Кожну точку з відрізка [0;1] можна подати у вигляді , .Отже, на першому кроці вилучаємо з розгляду точки з правого верхнього паралелограма. На другому – точки з паралелограмів, що знаходяться у правому верхньому куті паралелограмів, утворених на попередньому кроці. Продовжуючи цей процес, отримаємо точки серветки Серпінського (рис. 3.18).

Рис. 3.18. Перші три кроки побудови серветки Серпінського.

Спосіб 2. Інший спосіб аналітичного задання серветки Серпінського пропонує Працьовитий [20] (рис. 3.19).

Рис. 3.19.

Для побудови трикутника Серпінського беремо ряд r_n= , групу коренів 3-го степеня з одиниці x_n=cos +sin , 0,1,2…, а також точки з відрізка [0,1] в трійковій системі числення. Кожній точці з [0,1] ставимо у відповідність точку на комплексній площині, використовуючи ряд r_n та групу коренів 3-го степеня з одиниці x_k. (Після коми в представленні числа беремо нескінченну послідовність цифр).

Наприклад, точка на комплексній площині, яка відповідає точці 0,0121100... визначається наступним чином:

D⁽³⁾_0,0121100...=r₁x₀+r₂x₁+r₃x₂+r₄x₁+r₅x₁+r₆x₀+r₇x₀+...= x₀+ x₁+ x₂+ x₁+ x₁+

+ x….

3.6.4. С а м о п о д і б н і с т ь т р и к у т н о г о к и л и м а Серпінського. Трикутний килим Серпінского самоподібний. Позначимо частину килима Серпінского, яка належить трикутнику Т¹_і, через Т_і, і= 0,1,2. Зрозуміло, що

Т_с=Т₀ 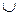Т₁ 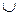Т₂ . (3.1)

Позначимо через h₁ перетворення гомотетії з центром у вершині А_і і коефіцієнтом гомотетії . Візьмемо одне з них, наприклад h₀ і переконаємося в тому, що при ньому килим Серпінского Т_с відображається на Т₀. Дійсно, при гомотетії трикутник Т¹_і рангу 1 переходить у трикутник Т²_0і рангу 2, і взагалі, трикутник Тⁿ_а1...аn… рангу n переходить при h₀ у трикутник Тⁿ_{0а1...аn...} рангу

Нехай точка має адресу . Їй відповідає послідовність вкладених трикутників

Т¹_а1 Т²_а1а2 ... Тⁿ_а1а2... ... (3.2)

Послідовність (3.2) при переходить також у послідовність вкладених один в одного трикутників:

Т¹₀ Т²_0а1 Т³_0а1а2 ... Т^а+n_{0а1а2...аn} ... (3.3)

Послідовності (3.3) відповідає точка х'=h₀(х), що також належить килиму. Адреса точки х' є 0а₁а₂...n....

Отже, під дією гомотетії h₀ кожна точка килима Т_с з адресою а₁а₂...n... переходить у точку килима х'=h₀(х) із Т₀ з адресою 0а₁а₂...n..., що починається з 0.

Вірне і зворотне: у будь-яку точку х' килима із Т₀, тобто в точку з адресою 0а₁а₂...n..., що починається з 0, переходить точка із наступною адресою: а₁а₂...n...

Таким чином, доведено, що h₀(Т_с)=Т₀. Тому що

Т_с=Т₀ 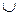Т₁ 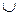Т₂=h₀(Т_с) 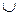h₁(Т_с) 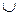h₂(Т_с),

килим Серпінского є об'єднання трьох гомотетичних йому образів і в цьому розумінні він самоподібний.

Дата добавления: 2015-08-21