Ц в и н т а р С е р п і н с ь к о г о

Описовий спосіб задання. Цю фігуру можемо отримати так: візьмемо квадрат, на першому кроці поділимо його на 9 конгруентних квадратиків і відкинемо центральний квадратик і 4 прилеглих до нього. На наступному кроці проробимо це з кожним квадратиком, що залишився, і т.д. В границі ми отримаємо деяку фігуру –цвинтар Серпінського (див. рис. 3.2).

Рис. 3.2.

Аналітичний спосіб задання. Цвинтар Серпінського аналітично задати можна двома способами. Перший спосіб – декартовий добуток множини Кантора , тобто .

Другий спосіб, за допомогою точок в трійковій системі числення, де .

Якщо або , то ми одержимо цвинтар Серпінського.

По-іншому аналітично цвинтар Серпінського можна задати так: позначимо множину його точок 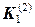(верхній індекс позначає розмірність простору, якому належать точки досліджуваної множини, нижній – будову елементів, які викидаємо, наприклад, якщо викидаємо сфери – індекс нуль, циліндри – одиниця, площини – двійка і т.д.), тоді:

Розмірність самоподібності. Порахуємо розмірність самоподібності цвинтаря Серпінського. Так як на першому етапі залишається 4 квадратики з подібністю до початкового, то підставивши ці дані в рівняння 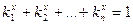(див. попередній випадок) одержуємо:

.

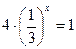Звідки .

Отже, розмірність самоподібності цвинтаря Серпінського рівна .

Дата добавления: 2015-08-21