Дослідження аналогів зірки Коха у тривимірному просторі

В цьому підрозділі досліджуються наступні узагальнення сніжинки Коха у тривимірному просторі:

1) циліндрична модель,

2) конічна модель,

3) брунькова модель,

4) каркас брунькової моделі.

Дослідження цих об’єктів ведеться за таким планом:

1) спосіб побудови,

2) фрактальна розмірність,

3) метричні властивості.

Крім того розглядаються інші властивості цих об’єктів. Результати досліджень взято з роботи Кулик С. В. [9] та Яковлевої О. П. [26].

2.6.1. Модель циліндричного виду. Розглянемо модель циліндричного виду, в основі якої лежить зірка Коха. В цій моделі площину зірки Коха буде давати лише переріз, паралельний основі отриманого циліндра.

Розглянемо процес побудови цієї фігури, знайдемо її розмірність, площу та об’єм, обмежений цією фігурою.

Процес побудови. Вихідна фігура – пряма призма, в основі якої лежить рівносторонній трикутник (рис. 2.25(а)), почнемо з однієї із граней призми. Нехай К₀ – початковий прямокутник. Розіб’ємо його двома відрізками на три рівних прямокутника, заберемо середній прямокутник і добудуємо два нових з тими ж самими параметрами. Отримаємо множину К₁ (рис. 2.25(б)). Повторимо цю процедуру багатократно. Позначимо через К_n – фігуру отриману на n-му кроці. Послідовність 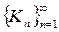збігається до деякої граничної фігури К. Назвемо її модель циліндричного виду.

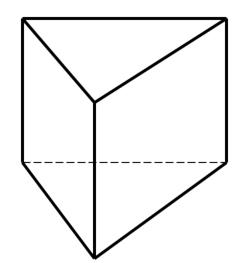
Рис. 2.25(а). Рис. 2.25(б).

Розмірність. Для того, щоб порахувати розмірність моделі циліндричного виду за К₀ візьмемо не прямокутник, а квадрат. Кожну грань вихідної фігури ділимо на 9 квадратів. На кожному із квадратів вертикальної смуги добудовуємо назовні правильну трикутну призму так, щоб цей квадрат був однією із граней призми. Утворена фігура зображена на рис. 2.26.

Рис. 2.26.

Таким чином, поділивши сторону вихідного квадрата на 3 (n=3), ми одержимо 12 квадратів нового етапу поділу (N=12). Тому:

Зовсім не обов’язково розглядати циліндричну модель, висота якої рівна стороні базового трикутника, при обчисленні фрактальної розмірності. Відомо, що фрактальна розмірність не змінюється при афінних перетвореннях простору, що дозволяє як завгодно змінювати висоту і кут нахилу твірних циліндра [27:21].

Площа поверхні та об’єм, обмежений даною фігурою. Нехай S₀ – площа вихідної фігури (прямої призми). Тоді площа кожної її грані. На першому кроці утворюється фігура, що має 12 граней, кожна з яких має площу , тому:

S ₁=

На другому кроці фігура має 48 граней, площа кожної грані – , тому:

S ₂= .

На n -му кроці:

S_n= .

Оскільки процес побудови на цьому кроці не завершується, то ми проводимо його нескінченно довго.

Обчислимо границю:

Отже, площа поверхні такого об’єкта нескінченно зростає.

Тепер знайдемо об'єм, обмежений цією фігурою.

Він дорівнює V=S_осн·Н. Оскільки частина площини, яку обмежує сніжинка Коха, має площу , де а – довжина початкового рівностороннього трикутника, то:

.

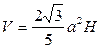Отже, наша фігура володіє такою властивістю: якщо процес побудови проводити нескінченно довго, площа поверхні такого об’єкта необмежено зростає, хоча об’єм, обмежений цією поверхнею, скінчений.

Дата добавления: 2015-08-21