
Означення 1.3. Нехай функція  визначена на підмножині
визначена на підмножині  простору
простору 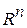 і приймає значення в
і приймає значення в  . Кажуть, що
. Кажуть, що  неперервна в точці
неперервна в точці 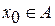 , якщо
, якщо
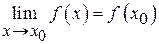 ,
,
тобто для кожного  існує таке число
існує таке число  , що з
, що з  , слідує
, слідує  .
.
Іншими словами, функція  неперервна в точці
неперервна в точці 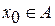 , якщо для кожної послідовності
, якщо для кожної послідовності 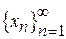 , що збігається до
, що збігається до  , існує границя
, існує границя
 . (1.1)
. (1.1)
Означення 1.4. Відображення 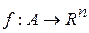 називається неперервним на
називається неперервним на  , або просто неперервним, якщо
, або просто неперервним, якщо  неперервна у всіх точках
неперервна у всіх точках  .
.
У загальному випадку функція  ставить у відповідність елементам одного метричного простору
ставить у відповідність елементам одного метричного простору 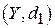 елементи іншого метричного простору
елементи іншого метричного простору 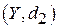 .
.
Нас цікавлять властивості вихідної множини  , які при неперервному відображенні
, які при неперервному відображенні  зберігаються без змін у множини
зберігаються без змін у множини  . Такі властивості будемо називати інваріантами неперервності.
. Такі властивості будемо називати інваріантами неперервності.
Означення 1.5. Множина 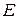 в
в  називається відносно відкритою в
називається відносно відкритою в  , якщо можна вказати таку відкриту множину
, якщо можна вказати таку відкриту множину  в
в 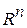 , що
, що  . Відповідно,
. Відповідно, 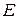 називається відносно замкненою в
називається відносно замкненою в  , якщо можна вказати таку замкнену множину
, якщо можна вказати таку замкнену множину  в
в 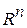 , що
, що  .
.
Наприклад, напіввідкритий інтервал  є відносно відкритим у множині
є відносно відкритим у множині 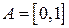 . Відносно замкненою множиною в
. Відносно замкненою множиною в 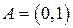 є напіввідкритий інтервал
є напіввідкритий інтервал 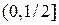 .
.
Нехай 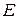 – підмножина області значень
– підмножина області значень  . Прообразом
. Прообразом 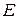 при відображенні
при відображенні  називається множина
називається множина
 .
.
Наприклад, якщо  то
то 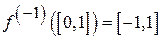 .
.
Перед тим, як перейти до основної теореми цього розділу, спочатку виведемо ряд важливих підтеорем, котрі потім ефективно зможемо використати при доведенні інваріантності множини Кантора.
Теорема 1.1. Відображення  з
з  на
на 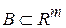 неперервне тоді і тільки тоді, якщо прообраз
неперервне тоді і тільки тоді, якщо прообраз  кожної множини
кожної множини 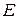 , відносно відкритої (відносно замкненої) в
, відносно відкритої (відносно замкненої) в 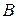 , відносно відкрита (відносно замкнена) в
, відносно відкрита (відносно замкнена) в  .
.
Доведення. (Випадок відносно відкритих множин.)
Достатність. Нехай 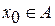 і
і  . Множина
. Множина 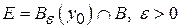 , відносно відкрита в
, відносно відкрита в 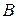 . Так як
. Так як 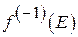 за умовою відносно відкрита в
за умовою відносно відкрита в  , то існує така відкрита множина
, то існує така відкрита множина  в
в 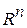 , що
, що 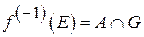 . Виберемо
. Виберемо 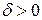 так, щоб
так, щоб 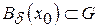 . Тоді
. Тоді  . А отже, відображення
. А отже, відображення  неперервне.
неперервне.
Необхідність. Нехай 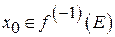 і
і 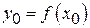 . Так як множина
. Так як множина 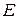 відносно відкрита в
відносно відкрита в 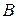 , то існує така відкрита множина
, то існує така відкрита множина  в
в  , що
, що  . Виберемо
. Виберемо 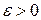 так, щоб
так, щоб 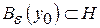 . Тоді
. Тоді  для деякого
для деякого 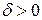 , внаслідок неперервності
, внаслідок неперервності  в точці
в точці  . Визначимо відкриту множину
. Визначимо відкриту множину  в
в 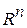 як об’єднання куль
як об’єднання куль  . Тоді
. Тоді  , і тому
, і тому 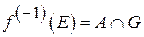 . А отже,
. А отже, 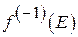 відносно відкрита в
відносно відкрита в  . Доведено.
. Доведено.
Доведення цієї теореми дає нам важливі наслідки.
Наслідок 1. Нехай  і
і 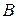 – відкриті множини. Відображення
– відкриті множини. Відображення 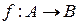 неперервне тоді і тільки тоді, якщо прообраз
неперервне тоді і тільки тоді, якщо прообраз 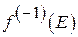 кожної відкритої множини
кожної відкритої множини 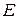 відкритий.
відкритий.
Доведення. Так як 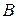 відкрита, а
відкрита, а 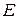 відносно відкрита в
відносно відкрита в 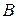 , то
, то 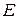 відкрита в
відкрита в 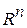 . За теоремою 1.1 для неперервності
. За теоремою 1.1 для неперервності  необхідно, щоб прообраз
необхідно, щоб прообраз 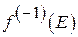 кожної множини
кожної множини 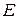 був відносно відкритий в
був відносно відкритий в  . Оскільки
. Оскільки  сама відкрита, то достатньо вимагати відкритості
сама відкрита, то достатньо вимагати відкритості 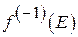 в
в 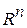 . Доведено.
. Доведено.
Наслідок 2. Нехай  і
і 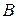 – замкнені множини. Відображення
– замкнені множини. Відображення 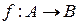 неперервне тоді і тільки тоді, якщо прообраз
неперервне тоді і тільки тоді, якщо прообраз 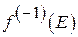 кожної замкненої множини
кожної замкненої множини 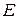 замкнений.
замкнений.
Доведення. Так як 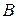 замкнена, а
замкнена, а 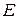 відносно замкнена в
відносно замкнена в 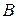 , то
, то 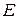 замкнена в
замкнена в 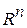 . За теоремою 1.1 для неперервності
. За теоремою 1.1 для неперервності  необхідно, щоб прообраз
необхідно, щоб прообраз 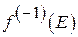 кожної множини
кожної множини 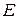 був відносно замкнений в
був відносно замкнений в  . Оскільки
. Оскільки  сама замкнена, то достатньо вимагати замкненості
сама замкнена, то достатньо вимагати замкненості 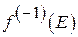 в
в 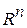 . Доведено.
. Доведено.
Далі покажемо, що наша множина С при неперервному відображенні f відобразиться в компактну множину. При доведенні розглянемо загальний випадок.
Теорема 1.2. Нехай  - компактна підмножина
- компактна підмножина 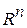 . Якщо відображення
. Якщо відображення 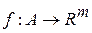 неперервне, то множина
неперервне, то множина 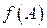 компактна.
компактна.
Доведення. В загальному випадку, множина є компактною, якщо з кожної послідовності точок можна виділити підпослідовність, що збігається до деякої точки даної множини. Нехай 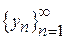 – послідовність з
– послідовність з 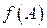 , а
, а 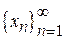 – послідовність з
– послідовність з  , причому
, причому
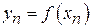
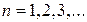 .
.
Так як  компактна, то з послідовності
компактна, то з послідовності 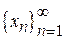 можна виділити підпослідовність
можна виділити підпослідовність 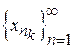 , що збігається до деякої точки
, що збігається до деякої точки 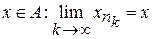 . З умови (1.1) слідує:
. З умови (1.1) слідує:
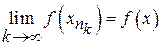 (1.2)
(1.2)
Таким чином, підпослідовність 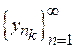 з
з 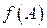 збігається до точки
збігається до точки  з
з 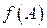 . Доведено.
. Доведено.
Теорема 1.3. Нехай  - зв’язна підмножина
- зв’язна підмножина 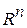 . Якщо відображення
. Якщо відображення 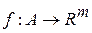 неперервне, то множина
неперервне, то множина 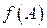 зв’язна.
зв’язна.
Доведення. По-перше, відмітимо, що множина 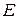 зв’язна тоді і тільки тоді, коли вона не є об’єднанням двох непорожніх неперерізних відносно відкритих в
зв’язна тоді і тільки тоді, коли вона не є об’єднанням двох непорожніх неперерізних відносно відкритих в 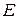 множин.
множин.
Припустимо, що множина 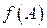 незв’язна. Тоді
незв’язна. Тоді  , де
, де  і
і  –непорожні неперерізні відносно відкриті в
–непорожні неперерізні відносно відкриті в 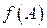 множини. За наслідком 1, множини
множини. За наслідком 1, множини 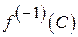 і
і 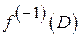 відносно відкриті в
відносно відкриті в  і не перетинаються, а тому множина
і не перетинаються, а тому множина 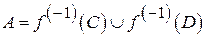 не є зв’язною, що суперечить умові. Доведено.
не є зв’язною, що суперечить умові. Доведено.
1.2.2. Т о п о л о г і ч н і і н в а р і а н т и. Дамо означення топологічної інваріантності. Якщо функція  відображає
відображає  на
на 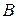 взаємно однозначно, то існує обернена функція
взаємно однозначно, то існує обернена функція 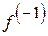 :
:
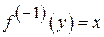 , де
, де  .
.
Наприклад, функція 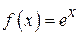 відображає дійсну пряму
відображає дійсну пряму 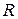 на
на  взаємно однозначно. Оберненою функцією для неї є
взаємно однозначно. Оберненою функцією для неї є 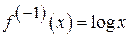 . В загальному випадку обернена функція може бути і розривною, навіть якщо функція
. В загальному випадку обернена функція може бути і розривною, навіть якщо функція  неперервна. Однак, якщо
неперервна. Однак, якщо  компактна, то функція
компактна, то функція 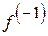 неперервна.
неперервна.
Означення 1.6. Взаємно однозначна неперервна функція, що має неперервну обернену, називається гомеоморфізмом або топологічним відображенням.
В цьому випадку множини  і
і 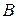 називаються гомеоморфними або топологічно еквівалентними. Властивості множин, які зберігаються при гомеоморфізмі, називаються топологічними інваріантами. Двома такими властивостями є компактність і зв’язність. Тут варто згадати також повну незв’язність та досконалість множин.
називаються гомеоморфними або топологічно еквівалентними. Властивості множин, які зберігаються при гомеоморфізмі, називаються топологічними інваріантами. Двома такими властивостями є компактність і зв’язність. Тут варто згадати також повну незв’язність та досконалість множин.
Наступна теорема дає можливість показати, що взаємно однозначне неперервне відображення компакту є гомеоморфізм. Оскільки множина С є компактною множиною, то дане доведення відноситься до неї безпосередньо і може бути використане нами при доведенні основної теореми.
Теорема 1.4. Якщо 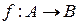 є взаємно однозначне неперервне відображення компакту
є взаємно однозначне неперервне відображення компакту  на
на 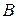 , то обернена функція
, то обернена функція 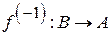 також неперервна, тобто
також неперервна, тобто  є гомеоморфізмом.
є гомеоморфізмом.
Доведення. За наслідком 2 з теореми 1.1, достатньо показати, що образ 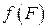 кожної замкненої множини
кожної замкненої множини 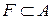 замкнений. Нехай
замкнений. Нехай 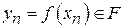 та
та 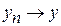 при
при 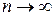 . Доведемо, що
. Доведемо, що 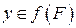 . Так як
. Так як  компактна, то існує підпослідовність
компактна, то існує підпослідовність 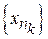 і така точка
і така точка  , що
, що 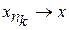 . Так як
. Так як  замкнена, то отримаємо
замкнена, то отримаємо 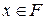 , і внаслідок неперервності
, і внаслідок неперервності  ,
, 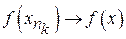 . З цього випливає, що
. З цього випливає, що  , і тому
, і тому 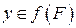 . Доведено.
. Доведено.
Дата добавления: 2015-08-21; просмотров: 128 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В е к т о р н а (арифметична) с у м а м н о ж и н К а н т о р а. | | | О с н о в н а т е о р е м а |