П о б у д о в а т а в л а с т и в о с т і.

Побудова пилу Кантора. Побудова класичного пилу Кантора починається з викидання середньої третини (не включаючи кінці) одиничного відрізку. Тобто вихідною множиною є відрізок [1, 0], і перший крок полягає в тому, що ми викидаємо відкритий інтервал (1/3, 2/3). На наступному і всіх інших етапах ми викидаємо середню третину (не включаючи кінці) всіх відрізків на даному рівні. Таким чином ми отримуємо (рис. 1.1) послідовність множин [8:39]:

С =[0,1]

С 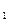=[0,1/3] 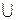[2/3,1]

С =[0,1/9] 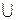[2/9,1/3] 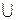[2/3,7/9] [8/9,1]

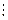
С.

Гранична множина С, що являє собою перетин множин С 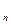, n = 0, …,i називається класичним пилом Кантора.

Рис. 1.1.

Канторів гребінь. Оскільки показати графічно пил Кантора надзвичайно важко в силу його розрідженості, то для наочності частіше використовують зображення (рис. 1.2), що є декартовим добутком множини С на відрізок якоїсь довжини. В даному випадку – на відрізок [0, 3]. В такому вигляді множина Кантора носить назву Канторового гребня.

Рис. 1.2.

Дата добавления: 2015-08-21