Cніжинка Коха

2.1. Означення сніжинки Коха

Означення 1. Нехай 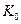– початковий відрізок (рис 2.1). Заберемо середню третину і додамо два нових відрізки такої самої довжини. Назвемо отриману множину 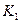. Повторимо цю процедуру багатократно, на кожному кроці заміняючи середню третину двома новими відрізками. Позначимо через 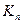фігуру, отриману після n-го кроку. Послідовність кривих збігається до деякої граничної кривої , яку називають сніжинкою Коха [8:17].

Рис. 2.1.

На рис. 2.2 показана сніжинка Коха після трьох кроків побудови.

Рис 2.2.

Означення 2. Сніжинкою Коха називається крива, кожна третина якої будується ітераційно, починаючи з однієї із сторін рівностороннього трикутника. Нехай 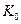– початковий відрізок (рис 2.1). Заберемо середню третину і додамо два нових відрізки такої самої довжини. До сніжинки Коха на цьому кроці належать точки 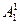, , 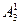(рис. 2.3). Повторимо цю процедуру багатократно, на кожному кроці заміняючи середню третину двома новими відрізками. На другому кроці сніжинці Коха крім вже названих будуть належати точки , , , , , , , , , , , .

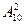На інших сторонах рівностороннього трикутника робимо аналогічні побудови і одержуємо відповідні точки сніжинки Коха. Після нескінченної кількості кроків отримаємо зліченну множину точок, зробивши замикання якої (множина вже матиме потужність континуум) і одержимо сніжинку Коха.

Аналітичне задання. Ідея наведеного нижче способу побудови та аналітичного задання сніжинки Коха запропонована Працьовитим М.В. [23].

Означення 3. Візьмемо послідовність : і множину коренів шостого степеня з одиниці , . Кожному числу , яке належить відрізку [0,1] і має нескінченну кількість цифр після коми, поставимо у відповідність точку комплексної площини

(2.1)

Введемо обмеження на вибір : , коли ; , коли , причому забороняються такі комбінації :

21, 22, 201, 202, 2001, 2002, 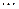; 45, 44, 404, 405, 4004, 4005, 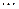(2.2)

Множина точок комплексної площини, утворена за правилом (2.1) із обмеженням (2.2) на вибір , утворить сніжинку Коха діаметром 2.

Змінюючи послідовність та групу комплексних коренів n -го степеня з 1, можна будувати різноманітні фрактали.

Дата добавления: 2015-08-21