В е к т о р н а (арифметична) с у м а м н о ж и н К а н т о р а.

Означення 1. Векторною сумою двох числових множин А і В (симв.: ) називається множина чисел виду , де , тобто

.

Якщо множина В складається тільки з одного числа , то векторна сума множин отримується зсувом множини А на одиниць вправо.

Лема 2. Векторна сума двох множин Кантора співпадає з відрізком [0;2].

Доведення. Очевидно, що векторна сума двох множин Кантора С належить відрізку [0;2]. Залишилось довести, що будь-яке число цього відрізку є сумою двох канторівських чисел.

Декартів добуток співпадає з “цвинтарем Серпінського” (див. розділ 3). Проведемо через довільну точку 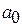відрізку [0;2] осі пряму 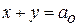, тобто пряму, нахилену до осі абсцис під кутом . Зрозуміло, що ця пряма перетне принаймні один з квадратів першого рангу (див рис. 1.5), по цій причині ця пряма перетне принаймні один квадрат другого рангу, третього і так далі. Звідки випливає, що вона проходить через деяку точку . А це значить, що , де . Отже, . Доведено.

Рис. 1.5.

1.1.5. В и з н а ч е н н я р о з м і р н о с т і м н о ж и н и С. Почнемо з розмірності Хаусдорфа – Безиковича. На 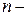му кроці канторівська множина E із Rⁿ складається з відрізків довжиною . Якщо спробувати вкрити множину прямолінійними відрізками довжини і розташувати їх акуратно, то нам вдасться вкрити всі відрізки 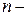го покоління, і отже, всі точки канторівської множини. Розглянемо всі можливі d-покриття прямолінійними відрізками, довжини яких не перевищує d, і кількість відрізків – зліченна. Тоді

це D -вимірна d-міра Хаусдорфа множини Е. А

де – D -міра Хаусдорфа. Якщо мале, то границя прямує до нескінченності, якщо велике, то границя прямує до нуля, якщо тільки ми не виберемо .

Величину D називають фрактальною (дробовою) розмірністю або розмірністю подібності. Явне вираження для D через N i l знаходиться логарифмуванням обох частин:

Знайдемо чому рівна топологічна розмірність класичної множини Кантора. Множина Кантора С є перетином вкладених множин С_к, k = 0,1, …, причому кожна множина С_к являє собою об’єднання 2^к замкнених неперекривних інтервалів довжиною 3^-к.

Нехай х, що належить С, а U – відносно відкрита множина, що містить х. Виберемо k так, щоб інтервал І С_к, в який попадає точка х, також належав U. Нехай V – відкритий інтервал, що містить I, але не має перетину з будь-яким з інших інтервалів, що утворюють С _к. Тоді Ø. Отже, топологічна (індуктивна) розмірність класичного пилу Кантора рівна 0.

Тополологічна розмірність самоподібної множини визначається величиною . Так як , ми заключаємо, що тріадна канторова множина є фрактальна множина з фрактальною розмірністю .

Канторівська множина, що описується тут, не зовсім самоподібна. Однак ми можемо розширити її за допомогою процедури інтерполяції, що охоплює область [0,3] двома канторівськими множинами, які вкривають інтервали [0,1] та [2,3]. Повторюючи цей процес необмежене число раз, ми можемо побудувати самоподібну множину на напівпрямій . Якщо змінити масштаб в рази, то, щоб покрити вихідну множину, нам знадобиться таких множин. З визначення розмірності подібності отримаємо 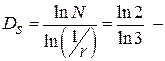розмірність подібності.

Розмірність подібності співпадає з фрактальною розмірністю тріадної канторівської множини.

Формула дозволяє тривіальним чином побудувати канторівську множину з довільно заданою розмірністю з інтервалу . На рисунку 1.6 показані дві різних побудови, які призводять до однієї і тієї ж розмірності D=1/2. Зовні дві множини виглядають по-різному, хоча вони обидві мають одну і ту ж фрактальну розмірність.

Рис. 1.6. Дві побудови канторівської множини з D=1/2. Зверху: N=2 і r=1/4; знизу N=3 і r=1/9

Можна зробити висновок, що для досить простої тріадної канторівської множини всі визначені вище різними способами розмірності співпадають.

Далі задамося питанням, що відбудеться коли два відрізка в елементі, що утворює канторівську множину, не будуть рівними? На рисунку 1.7 показано пил Кантора, який отримується, коли перший відрізок твірного елемента має довжину l₁=1/4, a другий l₂=2/5.

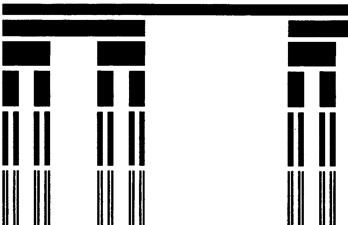
Рис. 1.7.

Обчислимо фрактальну довжину такої доволі простої канторівської множини .

Ця фрактальна множина може бути вкрита певним числом відрізків, що перетинаються . Нехай - евклідова довжина (діаметр) ї множини, так що вміщається в кубі з ребром . При розбитті з D -міра, використана для визначення розмірності Хаусдорфа – Безиковича, рівна

Критична розмірність, що отримується в границі при , є фрактальна розмірність даної множини. Розмірність подібності такої множини є розмірність, що задовольняє співвідношенню

В якості прикладу розглянемо множину Кантора, побудовану на рис.1.7. На n- му кроці число відрізків рівне N=2ⁿ. Найкоротший відрізок має довжину l₁ⁿ=(1/4)ⁿ, найдовший – l₂ⁿ=(2/5)ⁿ. Всього маємо (_kⁿ)=n!/k!(n-k)! відрізків довжиною l₁^kl₂^n-k при k=0,1,…,n. В n- му поколінні міра визначається виразом

Так як n 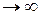при , ми можемо вважати, що міра залишається скінченною в тому і тільки тому випадку, коли D задовольняє співвідношенню

(l₁^D+l₂^D)=1.

Тобто при l₁=1/4 і l₂=2/5 маємо D=0.6110.

Дата добавления: 2015-08-21